et sa latitude 
.
(Voir aussi l'excellent article Représenter les mondes sur le même sujet, par Étienne Ghys.)
Le problème de la représentation plane de la Terre se pose depuis les anciens Grecs, au départ pour des problèmes de navigation. Et à juste titre : il est en effet impossible d'aplatir une sphère sans déchirure ni déformation, autrement dit il n'existe aucune application d'une sphère sur un plan conservant les distances, même localement, ni même aucun homéomorphisme entre une sphère complète et un plan.
Ici, comme le lecteur l'aura remarqué, on supposera la Terre sphérique
(cas plus simple et tout aussi intéressant, si ce n'est plus, qu'un
ellipsoïde ou qu'un géoïde). On repérera un point par sa longitude
et sa latitude .
Beaucoup de projections s'obtenaient au départ par des constructions
géométriques simples. Actuellement on utilise plutôt des équations
donnant directement la position du projeté à partir de
et 
.
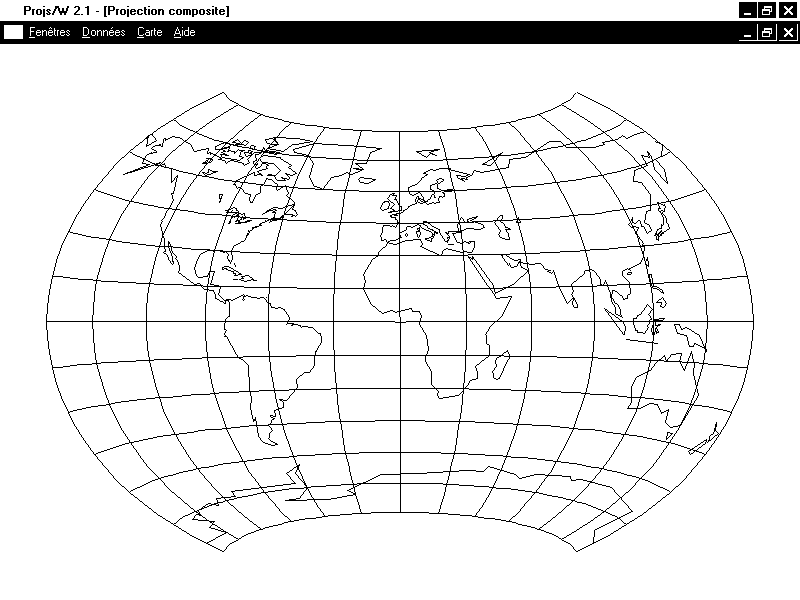
(Toutes les projections représentées ici ont été dessinées grâce au logiciel Projs, téléchargeable ici. Les méridiens ont été tracés avec un espacement de 30 degrés, et les parallèles avec un espacement de 15 degrés. Voir aussi le code du module de calcul du programme.)
Page suivante : Classification des projections