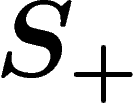 be any set (frequently
be any set (frequently 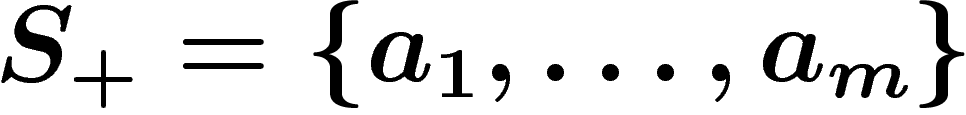 is finite).
Intuitively speaking, the free group on
is finite).
Intuitively speaking, the free group on 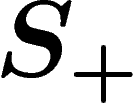 is the group consisting of
all formal products of elements of
is the group consisting of
all formal products of elements of 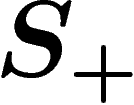 and their formal inverses, with
the cancellation
and their formal inverses, with
the cancellation 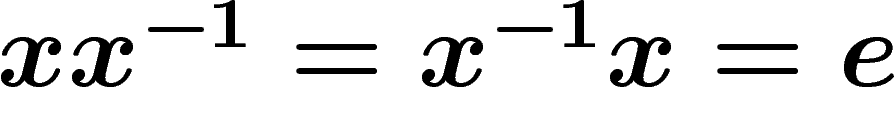 as the only computation rule.
as the only computation rule.
This text, originally written as an introduction to my book on random groups, gives an introduction to the study of discrete groups from a geometric point of view. It contains basic facts on group presentations and free groups; the construction of Cayley graphs and complexes; a sketch of what van Kampen diagrams are; and the different definitions of hyperbolic groups. An explicit example then gathers it all in two pictures.
We do not pretend to give an overview of geometric group theory as a whole, and many important aspects of the field are not mentioned.
A few selected references are given at the end as suggested reading.
From a geometric group theorist's viewpoint, which may not be everyone's, the simplest of all groups are free groups over some set of generators.
Let 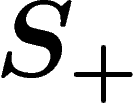 be any set (frequently
be any set (frequently 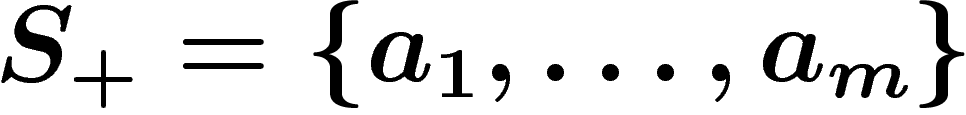 is finite).
Intuitively speaking, the free group on
is finite).
Intuitively speaking, the free group on 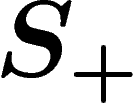 is the group consisting of
all formal products of elements of
is the group consisting of
all formal products of elements of 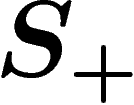 and their formal inverses, with
the cancellation
and their formal inverses, with
the cancellation 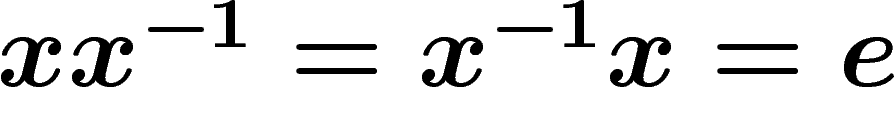 as the only computation rule.
as the only computation rule.
More precisely, let 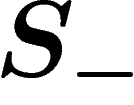 be the set of formal inverses
be the set of formal inverses 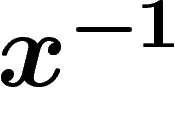 of the
elements
of the
elements 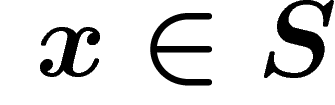 , which is just a distinct copy of
, which is just a distinct copy of 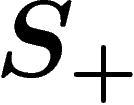 , and let
, and let
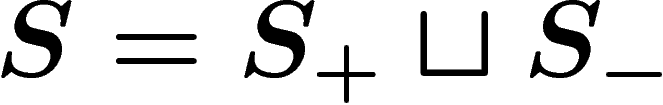 . For
. For 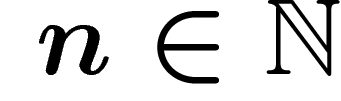 , a word of length n on
the alphabet S is a sequence of n elements of S. In the particular
case
, a word of length n on
the alphabet S is a sequence of n elements of S. In the particular
case 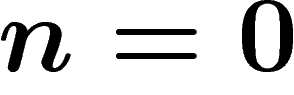 there is only one such sequence, called the empty word.
A word on S is just a word of any length, i.e. an element of
there is only one such sequence, called the empty word.
A word on S is just a word of any length, i.e. an element of
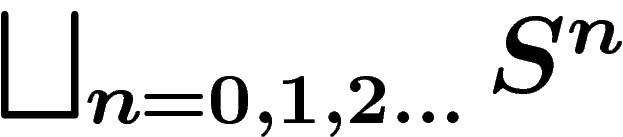 .
.
A word is said to be reduced if it does not contain as a subword
any sequence of the form 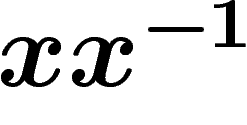 or
or 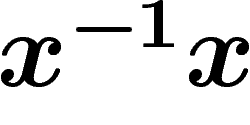 , for any
, for any 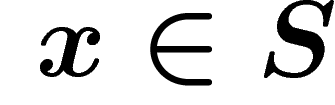 . With any
word can be associated a reduced word, by iterated removal of all such
cancellable pairs (the reduced word obtained does not depend on the order
in which removals are performed), an operation called reduction.
. With any
word can be associated a reduced word, by iterated removal of all such
cancellable pairs (the reduced word obtained does not depend on the order
in which removals are performed), an operation called reduction.
The free group generated by S (or by 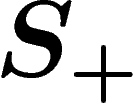 , terminology is
floppy) has all reduced words on S as its elements. Multiplication is
simply the concatenation of words, followed by reduction if necessary.
The neutral element e is the empty word.
, terminology is
floppy) has all reduced words on S as its elements. Multiplication is
simply the concatenation of words, followed by reduction if necessary.
The neutral element e is the empty word.
Of special importance is the case when 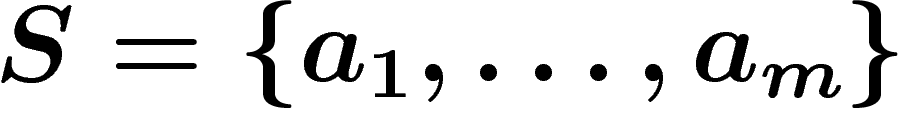 is finite;
the corresponding free group is denoted by
is finite;
the corresponding free group is denoted by 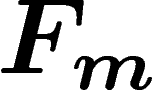 . When
. When 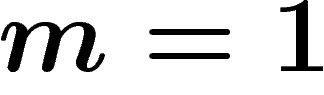 it is
isomorphic to the group of integers
it is
isomorphic to the group of integers  .
.
Now any group can be seen as a free group but with more ``computation
rules'' than simply 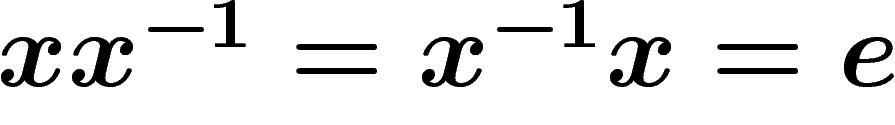 . This gives rise to the notion of
group presentations: a group specified by a given set of generators S,
with some ``enforced'' computation rules. For example, the
presentation
. This gives rise to the notion of
group presentations: a group specified by a given set of generators S,
with some ``enforced'' computation rules. For example, the
presentation 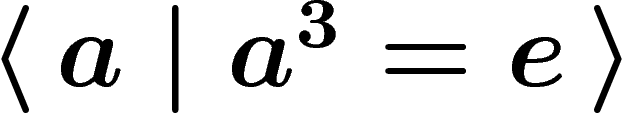 (read: the group generated by a,
knowing that
(read: the group generated by a,
knowing that 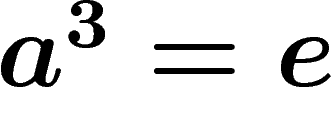 ) defines a group isomorphic to
) defines a group isomorphic to 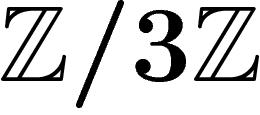 .
.
Namely, a computation rule is any equality 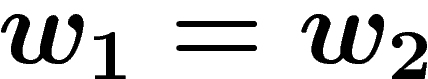 where
where 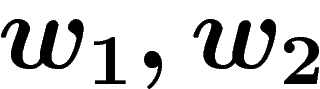 are
words on a given alphabet S. Any such rule can be rewritten
are
words on a given alphabet S. Any such rule can be rewritten
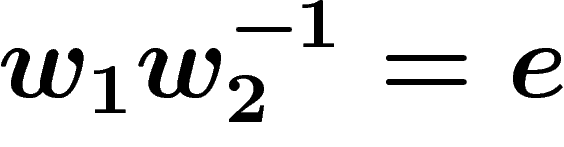 , and so most of the time rules are specified by giving
only one word r, with the rule
, and so most of the time rules are specified by giving
only one word r, with the rule  in mind.
in mind.
So let R be a set of words on a given alphabet 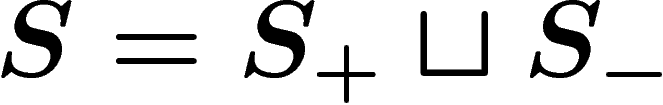 . The
group presented by
. The
group presented by 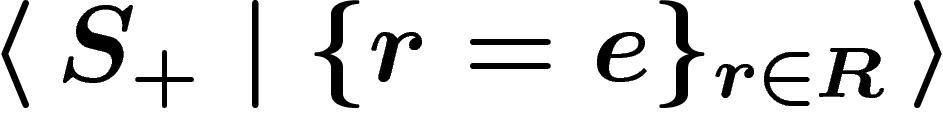 , or, more
simply, by
, or, more
simply, by 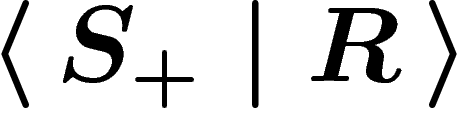 , is defined as follows. Start from the
free group
, is defined as follows. Start from the
free group 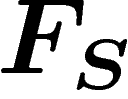 generated by
generated by 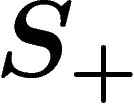 . The way to enforce a relation
. The way to enforce a relation  is to quotient
is to quotient 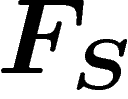 by the normal subgroup generated by r. So let
by the normal subgroup generated by r. So let
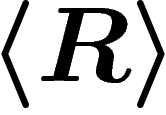 be the normal closure of the subgroup of
be the normal closure of the subgroup of 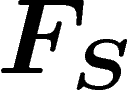 generated by all words
generated by all words 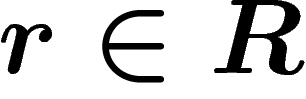 . The group presented by
. The group presented by
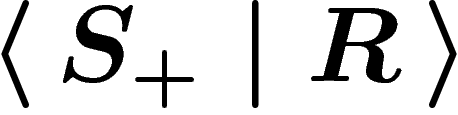 is the group
is the group 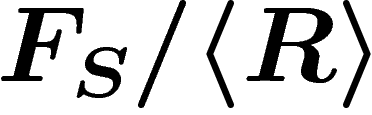 . It is the
``largest'' group in which all relations
. It is the
``largest'' group in which all relations  ,
, 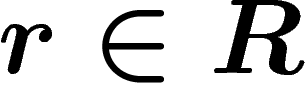 , hold.
, hold.
Let us give a few examples: the free group 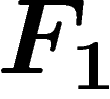 of rank one
(a.k.a.
of rank one
(a.k.a.  ) has the presentation
) has the presentation 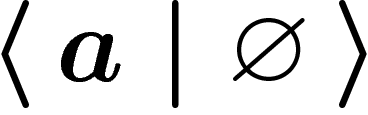 . The cyclic
groups
. The cyclic
groups 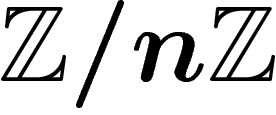 are given by
are given by 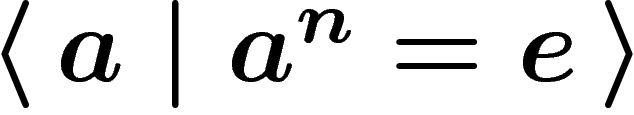 . The free
group of rank two is
. The free
group of rank two is 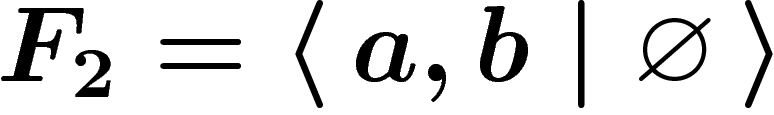 ; if we force a and
b to commute we get
; if we force a and
b to commute we get 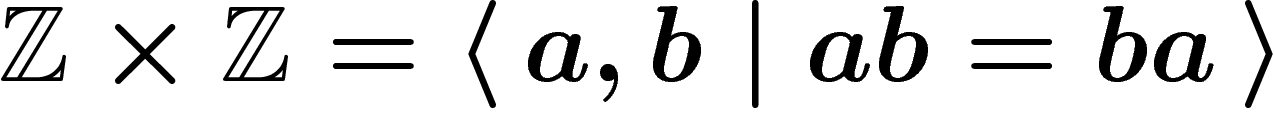 .
.
The elements of 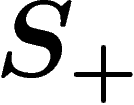 in a presentation
in a presentation 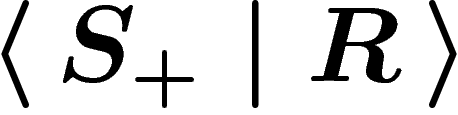 are called
generators. Those of R are called relators. It is easily
seen that relators can always be assumed to be reduced words.
are called
generators. Those of R are called relators. It is easily
seen that relators can always be assumed to be reduced words.
Note that any group has some presentation, in a kind of tautological way.
Let G be a group and take 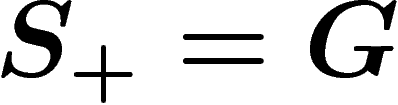 i.e. all elements of G will be
generators. Now let the set of words R consist of all products of
elements of S which happen to be equal to e in G. It is easy to
check that
i.e. all elements of G will be
generators. Now let the set of words R consist of all products of
elements of S which happen to be equal to e in G. It is easy to
check that 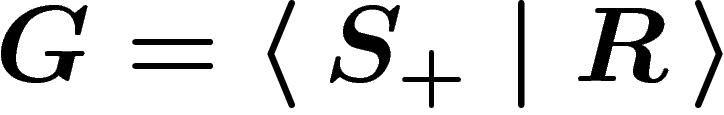 . (Of course this presentation is, in
general, way too large.)
. (Of course this presentation is, in
general, way too large.)
This means that free groups have a ``universal'' property, namely, for
each group G there is a set S and a surjective homomorphism from a
free group 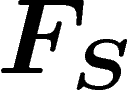 to G. More precisely, if
to G. More precisely, if  is any set which
generates G together with
is any set which
generates G together with 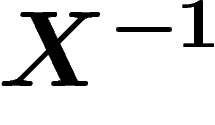 , then there is a surjective
homomorphism
, then there is a surjective
homomorphism 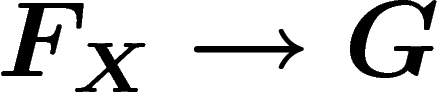 ``sending X to X'' i.e. sending an abstract
word in the generators to its image in G. If
``sending X to X'' i.e. sending an abstract
word in the generators to its image in G. If 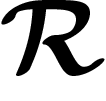 is the
kernel of this homomorphism, then any part
is the
kernel of this homomorphism, then any part  the
normal closure of which is
the
normal closure of which is 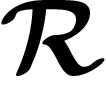 , will give rise to a
presentation
, will give rise to a
presentation 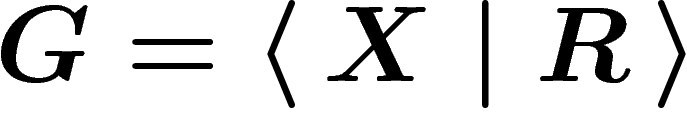 .
.
A group is finitely presented if it admits a presentation
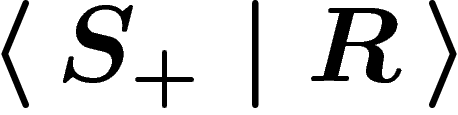 with both
with both 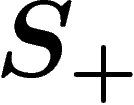 and R finite. A group is
finitely generated (or of finite type) if
and R finite. A group is
finitely generated (or of finite type) if 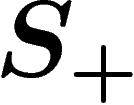 is finite.
is finite.
Presentations of a given group are by no means unique. For example, the
trivial group 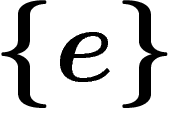 has arbitrarily (not so) stupid presentations such
as
has arbitrarily (not so) stupid presentations such
as 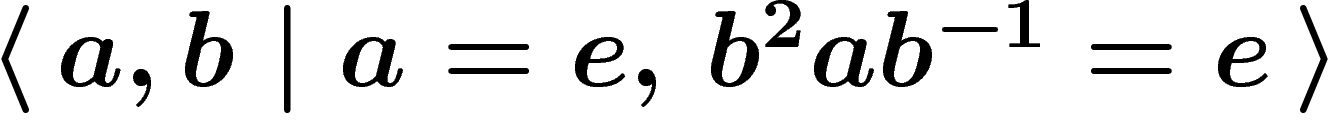 . (In fact it is not even
algorithmically decidable whether a given presentation defines the
trivial group or not!)
. (In fact it is not even
algorithmically decidable whether a given presentation defines the
trivial group or not!)
Hereafter, in order to get locally compact objects, we suppose that all sets of generators S are finite.
Cayley graphs. The above may seem quite combinatorial but
actually carries a geometrical meaning, which is sometimes a more natural
way to think of group presentations. For example, the group given by
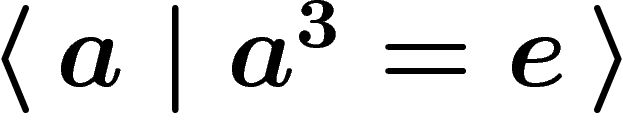 can be thought of as a three-edge cycle.
can be thought of as a three-edge cycle.
Let G be a group generated by a set  .
The Cayley graph of G with respect to S is the graph with
elements of G as vertices and in which edges correspond to
multiplication on the right by the generators.
.
The Cayley graph of G with respect to S is the graph with
elements of G as vertices and in which edges correspond to
multiplication on the right by the generators.
More precisely, the Cayley graph is an unoriented graph with some
decoration. Vertices are the elements of G. Now for each 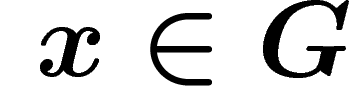 and
and
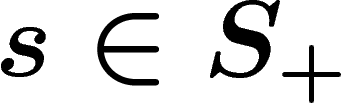 , add an unoriented edge between the vertices x and xs, so
that edges are in bijection with
, add an unoriented edge between the vertices x and xs, so
that edges are in bijection with  (this may result in
multiple edges and loops). Now keep track of this on the edges, by
deciding that with
each edge together with an orientation choice, will be associated a label in
(this may result in
multiple edges and loops). Now keep track of this on the edges, by
deciding that with
each edge together with an orientation choice, will be associated a label in
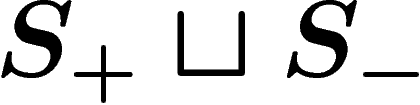 ; namely, the edge from x to xs, oriented this way,
will have label s, and label
; namely, the edge from x to xs, oriented this way,
will have label s, and label 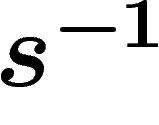 when oriented the other way
around*.
when oriented the other way
around*.
Basic examples are (w.r.t. the obvious generating sets): The Cayley
graph of the free group 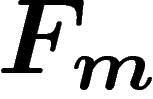 is an infinite tree in which each vertex
has valency
is an infinite tree in which each vertex
has valency 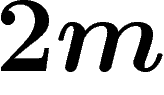 . The Cayley graph of the group
. The Cayley graph of the group  is an
infinite square grid in the plane. The Cayley graph of the cyclic group
of order n is an n-edge cycle.
is an
infinite square grid in the plane. The Cayley graph of the cyclic group
of order n is an n-edge cycle.
The Cayley graph is homogeneous: all vertices play the same role and could have been chosen to represent the neutral element e.
Given any vertex x in the Cayley graph and any word w on the alphabet S, we can start at x and track w in the graph by ``following the edge labels'', which brings us at xw. This path is called the lift of w (starting at x). Note that w is reduced if and only if this path has no local backtracks.
Left and right actions. The group G acts on the vertices of the Cayley graph in two ways: by left or right multiplication.
Left multiplication by 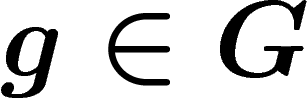 is a graph action: it brings adjacent
vertices to adjacent vertices, preserving edges. In particular it
preserves the graph distance. Note however that it does not bring a point
to a nearby point: x and gx can be very far away in the graph.
is a graph action: it brings adjacent
vertices to adjacent vertices, preserving edges. In particular it
preserves the graph distance. Note however that it does not bring a point
to a nearby point: x and gx can be very far away in the graph.
Conversely, right multiplication by 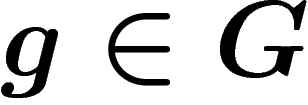 is not, in general, a graph
action, because a priori one does not pass from xg to xsg by
multiplication by s. So two points linked by an edge are not mapped to
two points linked by an edge: right multiplication acts only at the level
of vertices of the Cayley graph. However, right multiplication by g
moves a given point by a distance at most the length of g (since it
corresponds to following the path labelled by g in the Cayley graph,
starting at the given point).
is not, in general, a graph
action, because a priori one does not pass from xg to xsg by
multiplication by s. So two points linked by an edge are not mapped to
two points linked by an edge: right multiplication acts only at the level
of vertices of the Cayley graph. However, right multiplication by g
moves a given point by a distance at most the length of g (since it
corresponds to following the path labelled by g in the Cayley graph,
starting at the given point).
Consequently, when one mentions the action of G on its Cayley graph, it
is the left action which is meant. (Test all this in 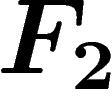 ...)
...)
Cayley complexes. It is worth noting that any word equal to
e in G will lift to a loop in the Cayley graph, and conversely. If
G is given by a presentation 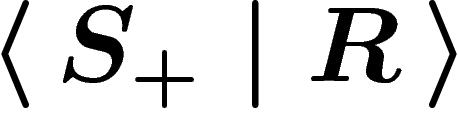 , this will be the
case, in particular, for the relators
, this will be the
case, in particular, for the relators 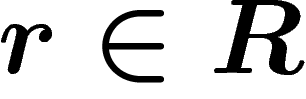 .
.
The Cayley complex of a presentation 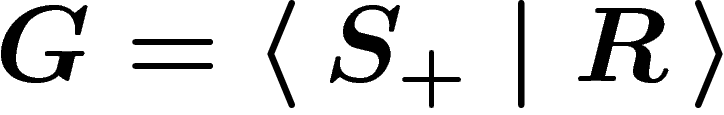 is a
is a
 -dimensional complex obtained by gluing a disk on all paths of the
Cayley graph labelled by a relator
-dimensional complex obtained by gluing a disk on all paths of the
Cayley graph labelled by a relator 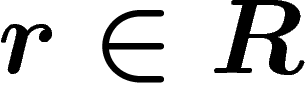 . More precisely, to each
. More precisely, to each
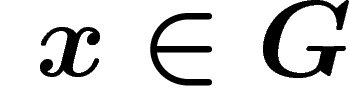 and
and 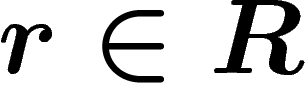 , consider the lift of r starting at x in the
Cayley graph, which is a closed path, and glue a disk along this path.
Consequently the set of faces of the Cayley complex is in bijection with
, consider the lift of r starting at x in the
Cayley graph, which is a closed path, and glue a disk along this path.
Consequently the set of faces of the Cayley complex is in bijection with
 .
.
Basic examples are (w.r.t. the usual presentations): The Cayley complex
of a free group is just its Cayley graph. The Cayley complex of  is the square tiling of the plane. The Cayley complex of the cyclic
group of order n consists of n disks sharing a common boundary (a
copy of the relation
is the square tiling of the plane. The Cayley complex of the cyclic
group of order n consists of n disks sharing a common boundary (a
copy of the relation 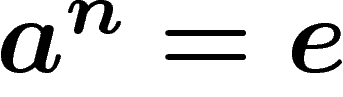 is glued to each element)*.
is glued to each element)*.
Most importantly, the Cayley complex is simply connected. Indeed, loops in the Cayley graph label words equal to the identity. Since by definition, relators generate all relations in the group, such words are exactly products of (conjugates of) relators in the presentation. We precisely added disks along loops of the Cayley graph representing the relators, making these loops homotopically trivial.
A word about classifying spaces. Here is another method to
define the Cayley graph and complex. Namely, consider a group
presentation 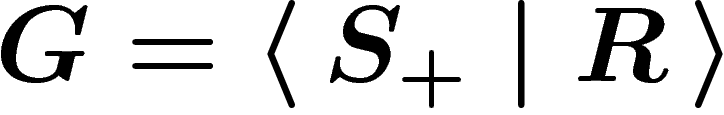 . There is a standard way to get a
topological space with fundamental group G. Start with a bouquet B of
. There is a standard way to get a
topological space with fundamental group G. Start with a bouquet B of
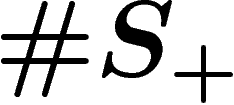 circles, that is, a graph made of one single vertex (denoted
e) and
circles, that is, a graph made of one single vertex (denoted
e) and 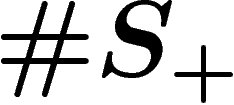 unoriented loops. Choose an orientation for each loop
and label loops bijectively by the generators in
unoriented loops. Choose an orientation for each loop
and label loops bijectively by the generators in 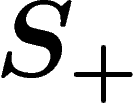 ; consider that the
loop with reverse orientation bears the inverse label in
; consider that the
loop with reverse orientation bears the inverse label in 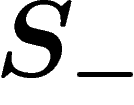 .
.
The fundamental group of this bouquet of circles is the free group with
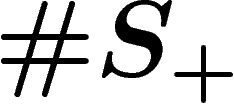 generators. The universal cover of this labelled graph is exactly the
Cayley graph of the free group on
generators. The universal cover of this labelled graph is exactly the
Cayley graph of the free group on 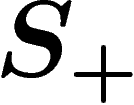 .
.
Now add ``relations'' in the following way. Any word on the alphabet
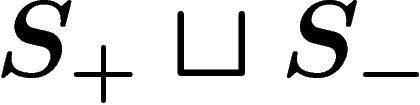 lifts to a closed path in the labelled graph B, just
as above for Cayley graphs. For each relator
lifts to a closed path in the labelled graph B, just
as above for Cayley graphs. For each relator 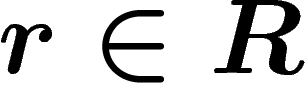 , add a disk to B
along the path labelled by r. In the fundamental group of B, this has
the effect of killing the element r. Thus at the end, one gets a
, add a disk to B
along the path labelled by r. In the fundamental group of B, this has
the effect of killing the element r. Thus at the end, one gets a
 -complex B (with one vertex,
-complex B (with one vertex, 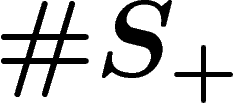 edges and
edges and 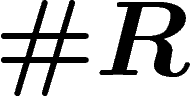 faces) the
fundamental group of which is precisely the group
faces) the
fundamental group of which is precisely the group 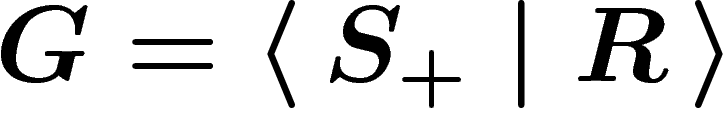 .
The universal cover of B is exactly the Cayley complex of this
presentation.
.
The universal cover of B is exactly the Cayley complex of this
presentation.
(By the way, if one goes on with this process and kill all the
higher-dimensional homotopy groups of B by adding sufficiently many
balls of dimension 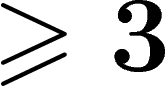 , one gets a so-called classifying
space for the group G, i.e. a space BG with fundamental group G
and such that the universal cover EG is contractible.)
, one gets a so-called classifying
space for the group G, i.e. a space BG with fundamental group G
and such that the universal cover EG is contractible.)
Here again all groups are assumed to be finitely generated.
Metrics on groups. The Cayley graph of a group w.r.t. some
generating set is naturally a metric space, defining each edge to have
length 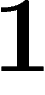 .
.
The combinatorial way to look at this is as follows: Given a group G
generated by a set of elements 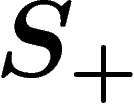 , it is natural to define the norm
, it is natural to define the norm
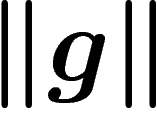 of an element
of an element 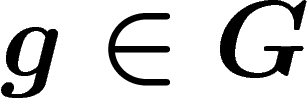 as the smallest length of a word
expressing g as a product of generators in
as the smallest length of a word
expressing g as a product of generators in 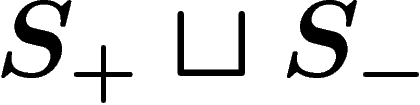 . This
coincides, of course, with the graph distance from g to e in the
Cayley graph of G w.r.t. this generating set. Note that
. This
coincides, of course, with the graph distance from g to e in the
Cayley graph of G w.r.t. this generating set. Note that
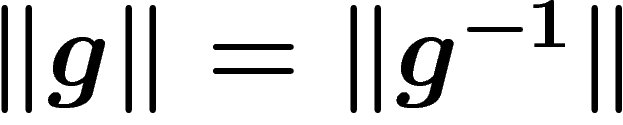 , and of course
, and of course 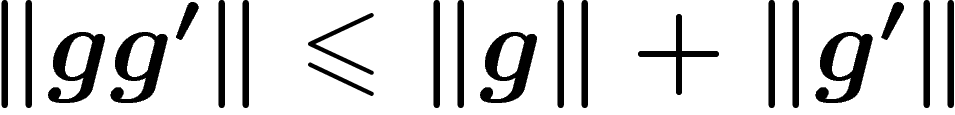 .
.
So we get a distance function on G by setting 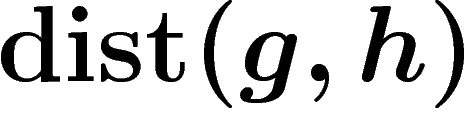 to be the
graph distance from g to h in the Cayley graph. Since edges of the
Cayley graph correspond to right multiplication by a generator, this is
the smallest length of a word w such that
to be the
graph distance from g to h in the Cayley graph. Since edges of the
Cayley graph correspond to right multiplication by a generator, this is
the smallest length of a word w such that 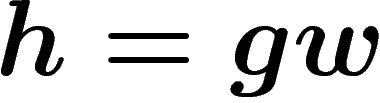 , that is,
, that is,
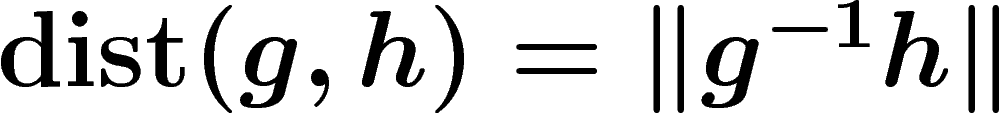 . The two properties of
. The two properties of  mentioned above are just the usual distance axioms.
mentioned above are just the usual distance axioms.
As mentioned above, the left action of G on itself preserves this metric.
Changing generators. Of course this distance depends on the chosen generating set. A finitely generated group is thus not equipped with a canonical metric, but with a family of metrics associated with all possible finite generating sets. These metrics are related in some way, which we explore now.
Let 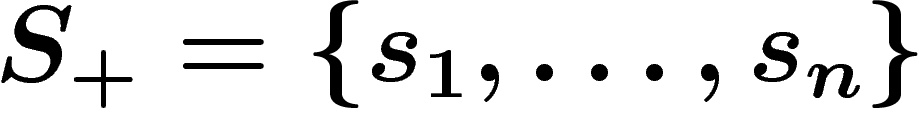 and
and 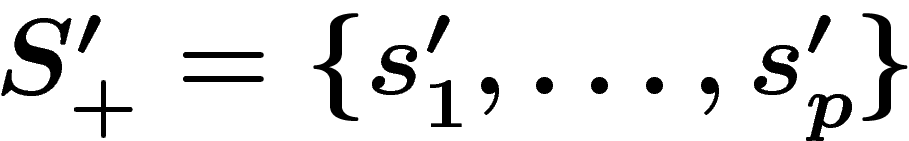 be two
finite generating sets for a group G; let
be two
finite generating sets for a group G; let 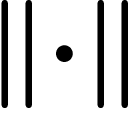 and
and
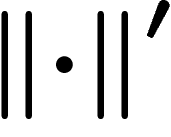 be the two associated norms. We want to control
be the two associated norms. We want to control
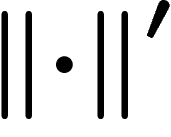 in terms of
in terms of 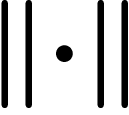 .
.
Since 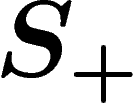 is a generating set, each of the elements in
is a generating set, each of the elements in 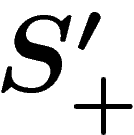 has a
writing in terms of the generators in
has a
writing in terms of the generators in 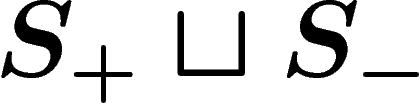 . Let K be the
largest length of such a writing i.e.
. Let K be the
largest length of such a writing i.e. 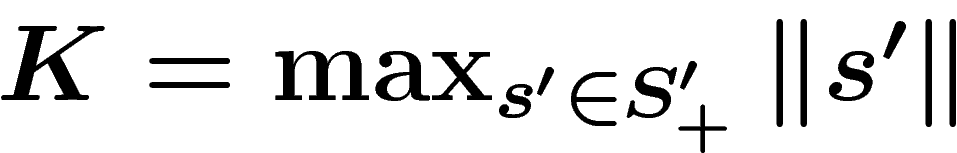 .
Since
.
Since  is finite, we have
is finite, we have  .
.
Now suppose that some element g has a writing of length n in
terms of  . By replacing each element of
. By replacing each element of  by a
writing of it in terms of
by a
writing of it in terms of 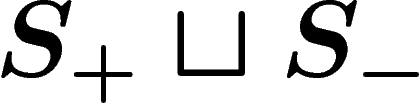 , we get a writing of g of length at
most Kn in terms of
, we get a writing of g of length at
most Kn in terms of 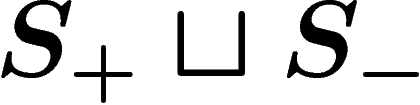 . So
. So 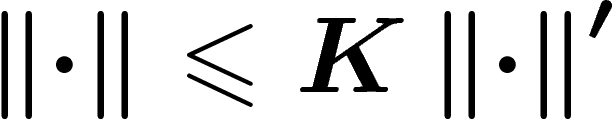 . The reasoning is two-sided, and so we get that the
metrics defined by
. The reasoning is two-sided, and so we get that the
metrics defined by 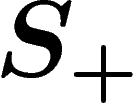 and
and 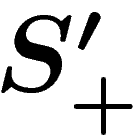 are bi-Lipschitz equivalent.
are bi-Lipschitz equivalent.
Quasi-isometries. Actually a slightly looser definition of
equivalence between metric spaces than bi-Lipschitz equivalence has
proven very fruitful: that of quasi-isometry. It allows, for
example, the spaces 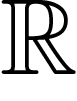 and
and  to be quasi-isometric, by neglecting
what happens at small scales.
to be quasi-isometric, by neglecting
what happens at small scales.
Let 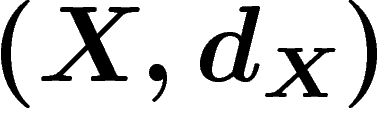 and
and 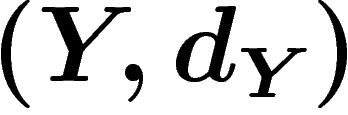 be two metric spaces. They are
quasi-isometric if there exist two maps
be two metric spaces. They are
quasi-isometric if there exist two maps 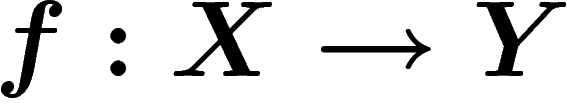 and
and 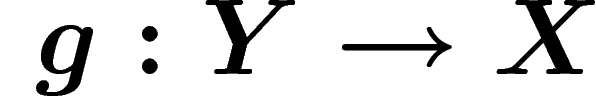 which distort distances in a linearly controlled way and which are almost
inverse to each other (up to a finite distance error). That is, there
exist constants
which distort distances in a linearly controlled way and which are almost
inverse to each other (up to a finite distance error). That is, there
exist constants 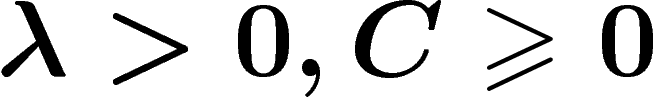 such that
such that
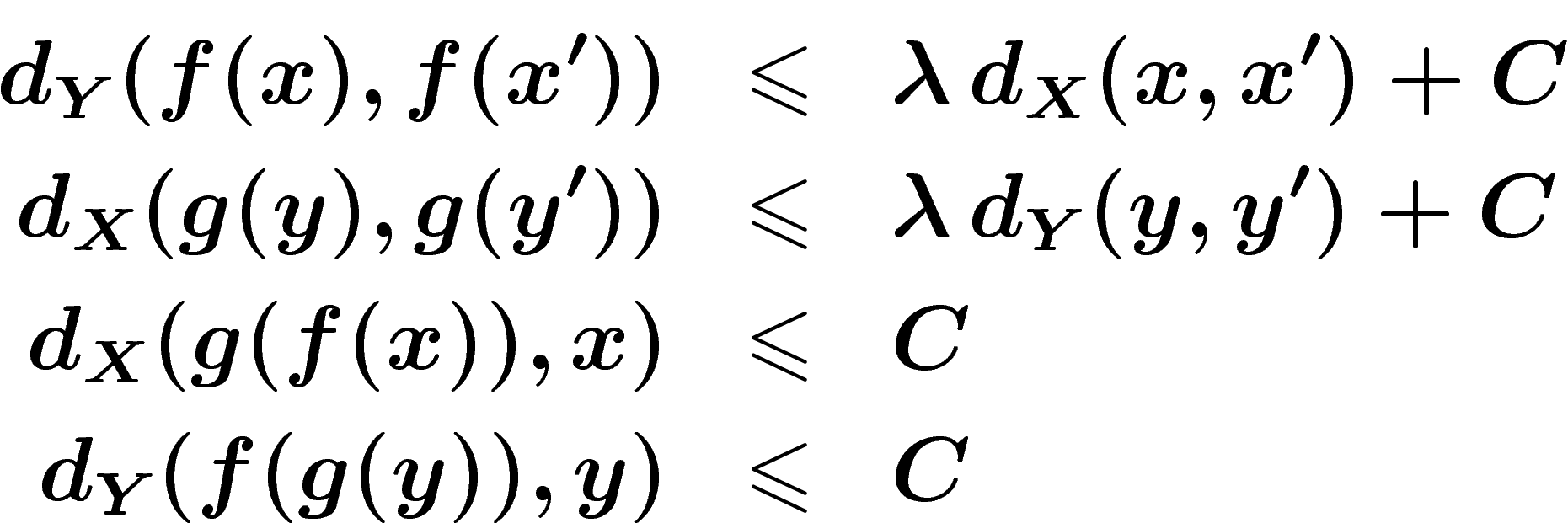
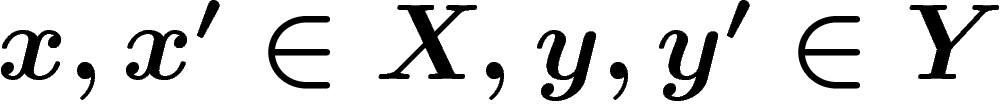 . This is an equivalence relation.
. This is an equivalence relation.
This notion is relevant for unbounded spaces only: any bounded metric space is quasi-isometric to a point.
A change in the generating set of a group is in particular a quasi-isometry. So any quasi-isometry invariant of a metric space, when applied to Cayley graphs, will provide a well-defined invariant of finitely generated groups.
Van Kampen diagrams are a visual way to represent how all equalities holding in a group are derived from combinations of relators.
Let 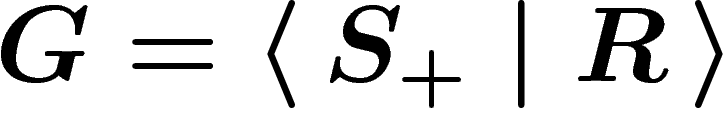 be a group presentation. Since we only have
access to elements of G as products of generators, we want to know when
two words represent the same element of G, i.e. we are interested in
the set of equalities of words
be a group presentation. Since we only have
access to elements of G as products of generators, we want to know when
two words represent the same element of G, i.e. we are interested in
the set of equalities of words 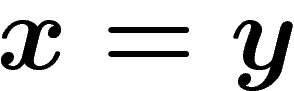 that hold in G. Since this can be
rewritten as
that hold in G. Since this can be
rewritten as 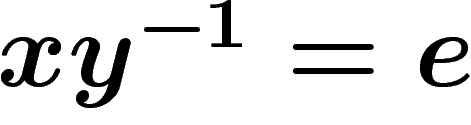 , it is enough to determine the set of words
representing the identity element of G (so-called word problem).
, it is enough to determine the set of words
representing the identity element of G (so-called word problem).
This problem is actually algorithmically unsolvable: there is no algorithm that, given any finite presentation and any word, always answers whether the given word is equal to e in the presentation. Moreover, this already holds for some fixed groups: there exist some group presentations for which there is no algorithm which, given any word, answers whether or not it is equal to e in the presentation.
A word is equal to e in the group G presented by
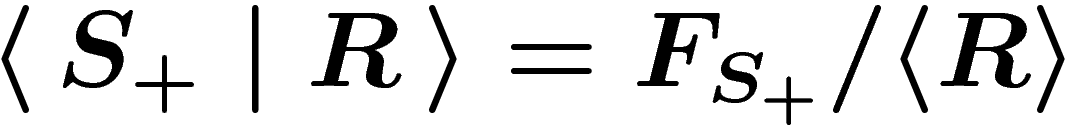 , by definition, if it lies
in the kernel of the map
, by definition, if it lies
in the kernel of the map 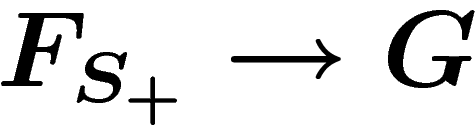 , that is, in the normal subgroup
, that is, in the normal subgroup 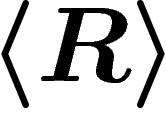 generated by the relators. Hence, a word w is equal to e in
G if and only if, as a word, it can be written as a product of
conjugates of relators:
generated by the relators. Hence, a word w is equal to e in
G if and only if, as a word, it can be written as a product of
conjugates of relators:
![\[
w=\prod_{i=1}^{N} u_i\,\, r_i^{\pm 1}\, u_i^{-1}
\]](primer153.png)
 and
and 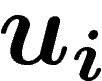 is any word. (The number N of relators in
this decomposition, which depends on w, will play an important role
below in the definition of hyperbolic groups.)
So algebraically speaking, the set of consequences of the relators is the
normal closure of the subgroup they generate. Van Kampen diagrams are a
visual interpretation of these products of conjugates.
is any word. (The number N of relators in
this decomposition, which depends on w, will play an important role
below in the definition of hyperbolic groups.)
So algebraically speaking, the set of consequences of the relators is the
normal closure of the subgroup they generate. Van Kampen diagrams are a
visual interpretation of these products of conjugates.
Giving a topologically clean definition of van Kampen diagrams is beyond
the scope of this review. Basically, the idea is to consider each
relator 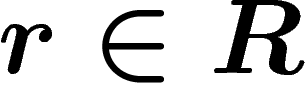 as a polygon with as many edges as letters in r, the
edges of which are labelled with the successive letters of r (the
inverse of r may also be used to build a polygon with reverse
orientation). Here is the polygon associated with the simple relator
as a polygon with as many edges as letters in r, the
edges of which are labelled with the successive letters of r (the
inverse of r may also be used to build a polygon with reverse
orientation). Here is the polygon associated with the simple relator
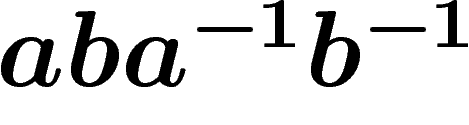 (starting at bottom left corner, counterclockwise):
(starting at bottom left corner, counterclockwise):
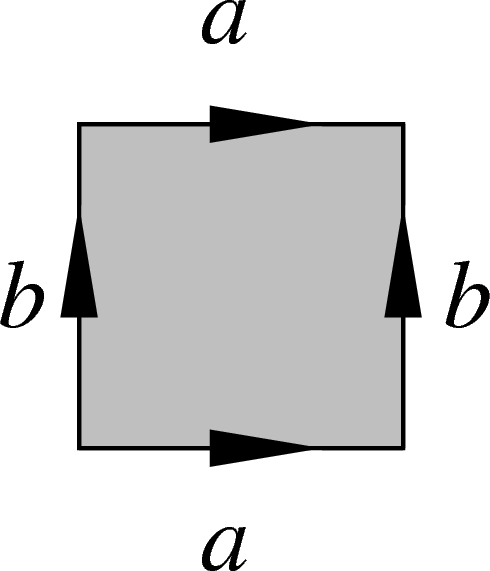
Now polygons bearing (same or different) relators can be glued to each
other along edges bearing the same letter. Van Kampen diagrams are the
figures resulting from such connected, simply connected gluings of
relator-bearing polygons. For example, the following van Kampen diagram
w.r.t. the presentation 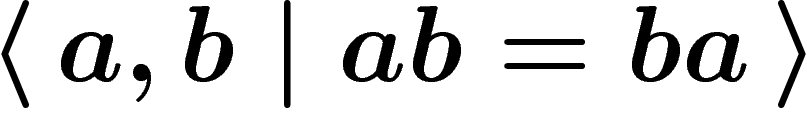 (i.e. with the only
relator
(i.e. with the only
relator 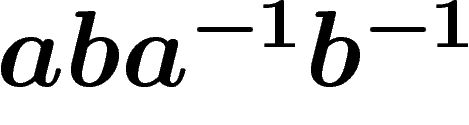 ) is a visual proof that if a commutes with
b, then so does
) is a visual proof that if a commutes with
b, then so does  .
.
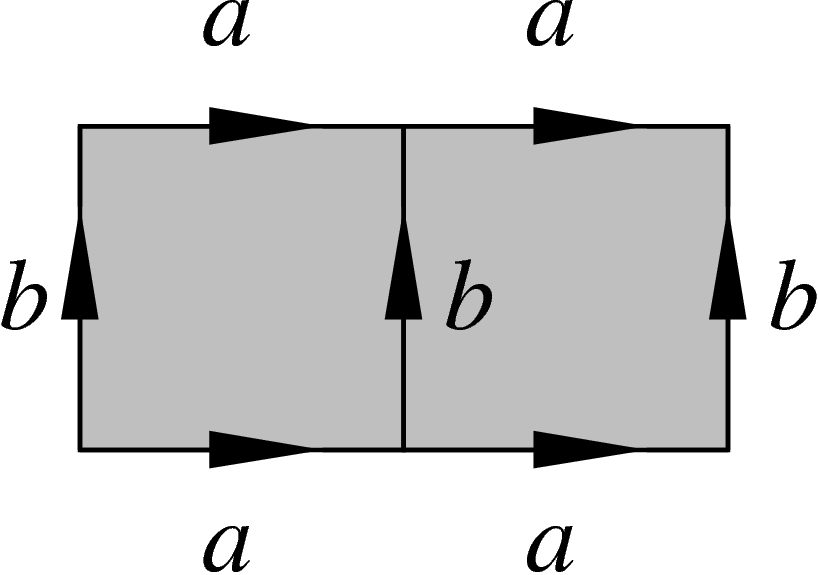
An important theorem of van Kampen states that the boundary words of such planar diagrams are exactly those words equal to e in the presentation.
The connection with products of conjugates of relators is clear on the
following picture, which builds the boundary word 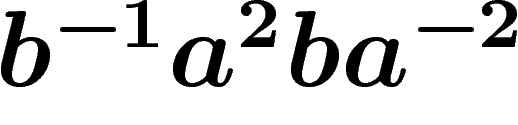 of
the van Kampen diagram given above (starting at top left corner,
counterclockwise) as a product
of
the van Kampen diagram given above (starting at top left corner,
counterclockwise) as a product 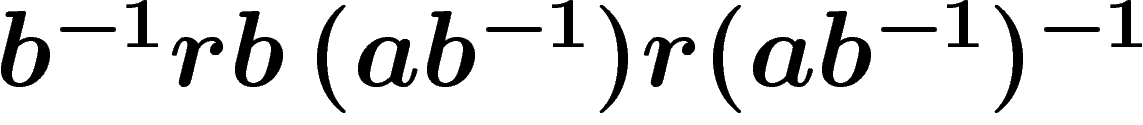 of
conjugates of the relator
of
conjugates of the relator 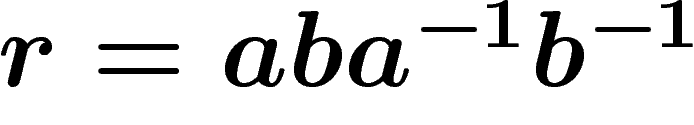 . Shrinking this diagram (by identifying edges
arising from the same point with the same label) produces the
two-square one above.
. Shrinking this diagram (by identifying edges
arising from the same point with the same label) produces the
two-square one above.
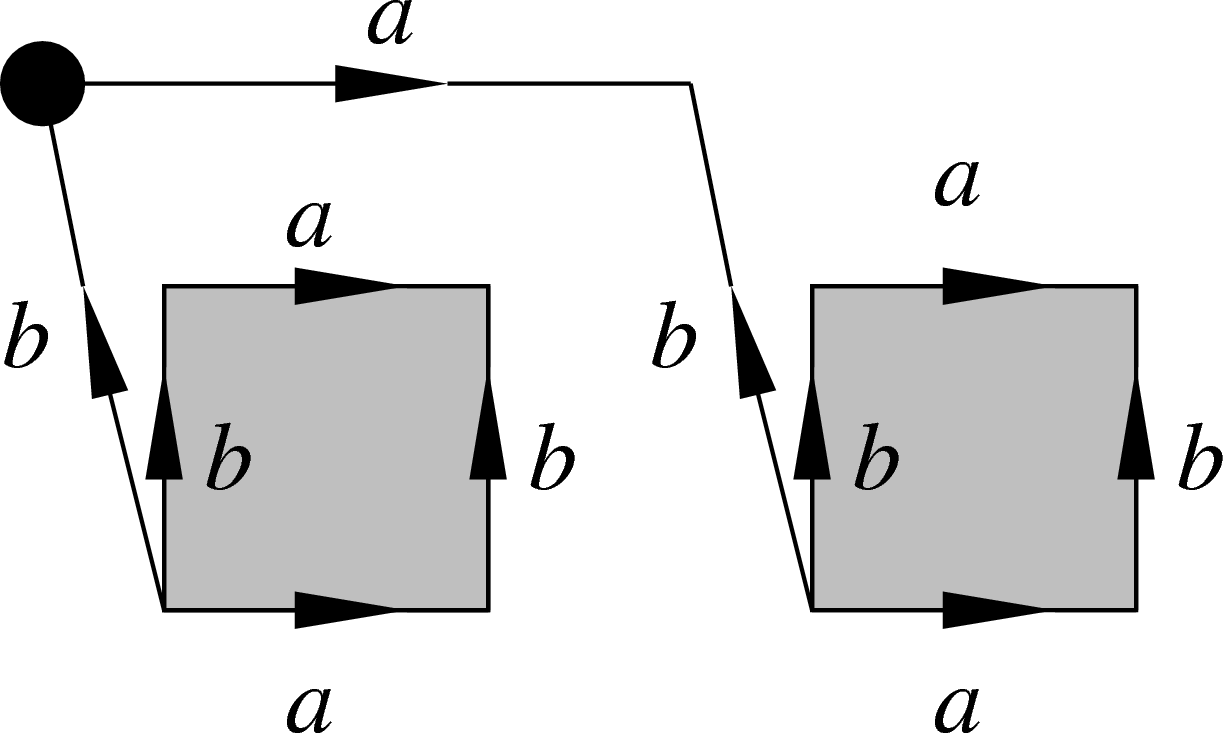
Incidentally, coming back to the algorithmic decidability problems mentioned above, we see that the word problem is semi-decidable: if a word is indeed equal to e, then, searching through all van Kampen diagrams, we will eventually find one decomposing the word as a product of conjugates of relators; but proving that the word is not equal to e would a priori require examination and rejection of all possible diagrams.
A class of groups the interest for which has never declined over the years
since its introduction by Gromov is that of hyperbolic groups.
They have a combinatorial definition, word hyperbolicity, and a
geometric one, 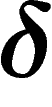 -hyperbolicity. Since (spoiler!) these two notions
have turned out to be equivalent, we simply use the term
hyperbolic.
-hyperbolicity. Since (spoiler!) these two notions
have turned out to be equivalent, we simply use the term
hyperbolic.
Word hyperbolicity. Let  be
a group with finite presentation. Recall that any word w equal to e
in G can be written as a product
be
a group with finite presentation. Recall that any word w equal to e
in G can be written as a product
![\[
w=\prod_{i=1}^{N} u_i r_i^{\pm 1} u_i^{-1}
\]](primer169.png)
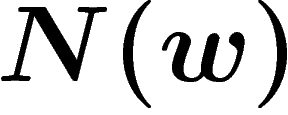 be the minimal number of relators in such a writing of
w. A very natural question is: How does
be the minimal number of relators in such a writing of
w. A very natural question is: How does 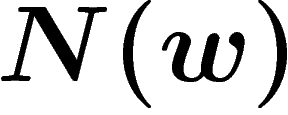 behave when the length
of w grows larger and larger?
behave when the length
of w grows larger and larger?
The presentation is said to be word-hyperbolic if 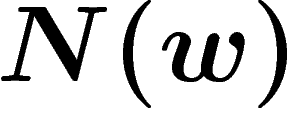 grows at
most linearly with the length of w, that is, if there exists a constant
C such that for any w we have
grows at
most linearly with the length of w, that is, if there exists a constant
C such that for any w we have  .
.
It is not difficult to see that for finite presentations, this linearity does not depend on the presentation chosen for a given group G: indeed, each generator in the second presentation is a product of (finitely many) generators in the first one, and each relator in the second presentation is a consequence of (can be written as products of conjugates of) finitely many relators in the first one, so that, since the number of generators and relators is finite, the constant C is perturbed by at most these quantities. So this yields a well-defined notion of a word-hyperbolic group.
When thought of in terms of van Kampen diagrams, this reads as follows:
If w is a word equal to e in the group, then there is a van Kampen
diagram D with w as its boundary word. Now by definition 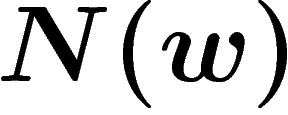 is the number of
faces
is the number of
faces 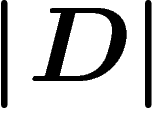 of this van Kampen diagram and the length of w is the
boundary length
of this van Kampen diagram and the length of w is the
boundary length 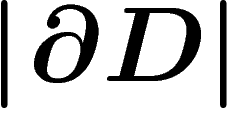 . So the word hyperbolicity condition
rewrites as
. So the word hyperbolicity condition
rewrites as
![\[
\abs{D}\leq C\abs{\partial D}
\]](primer177.png)
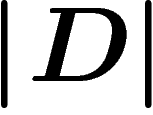 and boundary length standing for
and boundary length standing for 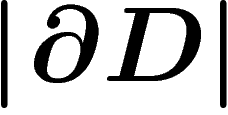 ), but not
by domains in the Euclidean plane (where boundary length grows only like the
square root of area).
), but not
by domains in the Euclidean plane (where boundary length grows only like the
square root of area).
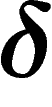 -hyperbolicity. This is a more general notion defined
in any geodesic space (that is, a metric space in which the
distance between two points is realized by one or several paths between
them, called geodesic segments). Since any graph is a geodesic
space (by definition, edge-paths realize the distance), it can be applied
to Cayley graphs of groups.
-hyperbolicity. This is a more general notion defined
in any geodesic space (that is, a metric space in which the
distance between two points is realized by one or several paths between
them, called geodesic segments). Since any graph is a geodesic
space (by definition, edge-paths realize the distance), it can be applied
to Cayley graphs of groups.
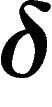 -hyperbolicity is a way to measure how ``negatively curved'' or
``tree-like'' a space looks at large scale. In a traditional negative
curvature setting, triangles have the property that the sum of their
angles is less than
-hyperbolicity is a way to measure how ``negatively curved'' or
``tree-like'' a space looks at large scale. In a traditional negative
curvature setting, triangles have the property that the sum of their
angles is less than 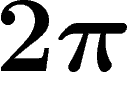 : they are curved inwards. This is measured by
Rips' condition of thinness of triangles.
: they are curved inwards. This is measured by
Rips' condition of thinness of triangles.
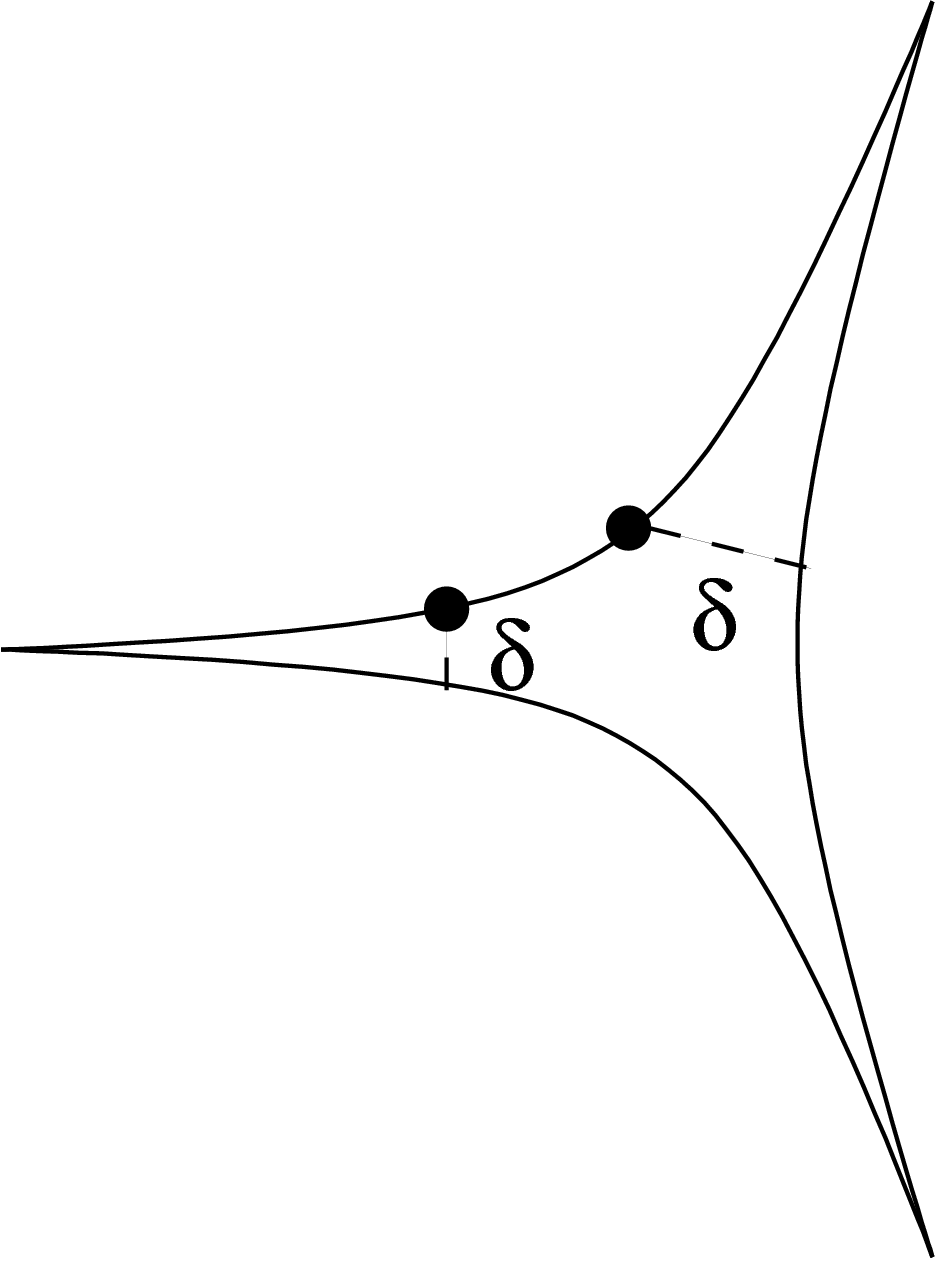
A triangle in a geodesic space is specified by a triple of points
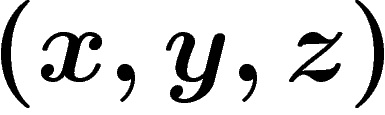 together with three geodesic segments joining them pairwise,
noted
together with three geodesic segments joining them pairwise,
noted ![$[xy]$](primer184.png) ,
, ![$[yz]$](primer185.png) and
and ![$[zx]$](primer186.png) . For
. For 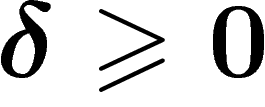 , the triangle is said
to be
, the triangle is said
to be 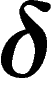 -thin if any point on
-thin if any point on ![$[xy]$](primer189.png) lies at distance at
most
lies at distance at
most 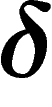 from the union
from the union ![$[yz]\cup[zx]$](primer191.png) of the two other sides, and
similarly for points on
of the two other sides, and
similarly for points on ![$[yz]$](primer192.png) , on
, on ![$[zx]$](primer193.png) . That is, the ``gap'' at the
middle of the triangle has size roughly
. That is, the ``gap'' at the
middle of the triangle has size roughly 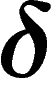 : each side does not
depart too much from the other two.
: each side does not
depart too much from the other two.
For 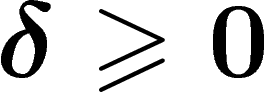 , a geodesic space is said to be
, a geodesic space is said to be
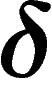 -hyperbolic (or simply hyperbolic if
-hyperbolic (or simply hyperbolic if 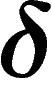 is
not specified) if any triangle in it is
is
not specified) if any triangle in it is 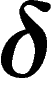 -thin. Note that this
must hold for all choices of geodesics between the vertices in case there
are several.
-thin. Note that this
must hold for all choices of geodesics between the vertices in case there
are several.
The usual hyperbolic plane is hyperbolic indeed (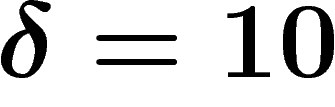 works).
Any bounded metric space is
works).
Any bounded metric space is 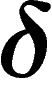 -hyperbolic (take its diameter as
-hyperbolic (take its diameter as
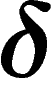 ). The Euclidean plane or the grid
). The Euclidean plane or the grid  are not hyperbolic for
any
are not hyperbolic for
any 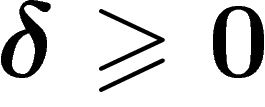 .
.
Another important example is a (finite or infinite) tree, which is
 -hyperbolic (triangles are flattened). In fact,
-hyperbolic (triangles are flattened). In fact, 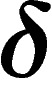 -hyperbolic
spaces are those which, ``seen from far away'', look like trees; they can
actually by approximated by trees (up to
-hyperbolic
spaces are those which, ``seen from far away'', look like trees; they can
actually by approximated by trees (up to 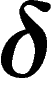 ) in a very precise
sense.
) in a very precise
sense.
Now a finite group presentation is 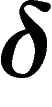 -hyperbolic if the
associated Cayley graph is. The most basic examples (apart from finite
groups) are the free groups
-hyperbolic if the
associated Cayley graph is. The most basic examples (apart from finite
groups) are the free groups 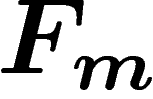 , whose Cayley graphs w.r.t. the
standard generating set are trees, hence
, whose Cayley graphs w.r.t. the
standard generating set are trees, hence  -hyperbolic. Hyperbolic
groups are thus a natural geometric generalization of free groups.
-hyperbolic. Hyperbolic
groups are thus a natural geometric generalization of free groups.
Importantly (but not obviously), 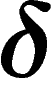 -hyperbolicity for some
-hyperbolicity for some
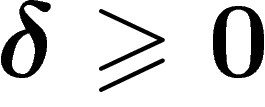 is preserved under quasi-isometries, although the value of
is preserved under quasi-isometries, although the value of
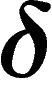 may change. In particular, for a group it does not depend on the
choice of a generating set.
may change. In particular, for a group it does not depend on the
choice of a generating set.
Hyperbolicity. A finitely presented group is word-hyperbolic if
and only if it is 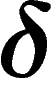 -hyperbolic for some
-hyperbolic for some 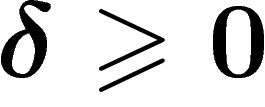 . This is a
non-trivial theorem and may actually be the shortest way to show that
. This is a
non-trivial theorem and may actually be the shortest way to show that
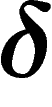 -hyperbolicity does not depend on the presentation of a given
group (though the value of
-hyperbolicity does not depend on the presentation of a given
group (though the value of 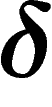 does).
does).
Note that we have defined word hyperbolicity only for group
presentations, whereas 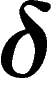 -hyperbolicity makes sense in a more
general context; but the notion of linear isoperimetric inequality of van
Kampen diagrams can be extended to any geodesic space and is still
equivalent to
-hyperbolicity makes sense in a more
general context; but the notion of linear isoperimetric inequality of van
Kampen diagrams can be extended to any geodesic space and is still
equivalent to 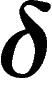 -hyperbolicity.
-hyperbolicity.
Small cancellation. The small cancellation conditions are
simple combinatorial criteria on a group presentation which imply
hyperbolicity. Maybe the one most frequently encountered is the
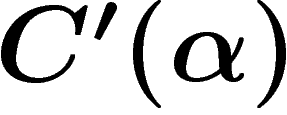 condition. Remember the idea of van
Kampen diagrams: relators in a presentation are represented as polygons
with boundary labelled by the relator. Now if two such polygons have a
common subword on their boundary (more precisely, if there is a word w
such that w is a subword of the boundary word of the first polygon and
condition. Remember the idea of van
Kampen diagrams: relators in a presentation are represented as polygons
with boundary labelled by the relator. Now if two such polygons have a
common subword on their boundary (more precisely, if there is a word w
such that w is a subword of the boundary word of the first polygon and
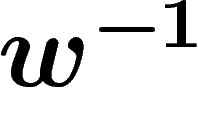 is a subword of the boundary word of the second one), we can
glue them along this subword to form a two-face van Kampen diagram.
is a subword of the boundary word of the second one), we can
glue them along this subword to form a two-face van Kampen diagram.
The 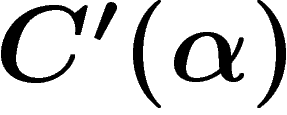 condition for a presentation (for
condition for a presentation (for 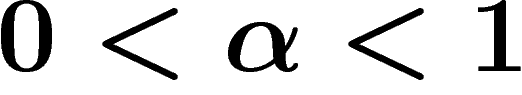 ) demands
that any such gluing between two polygons bearing relators
) demands
that any such gluing between two polygons bearing relators 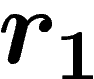 and
and
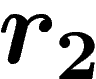 in the presentation occurs along a path w of length less than
in the presentation occurs along a path w of length less than
 times the infimum of the lengths of
times the infimum of the lengths of 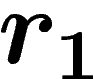 and
and 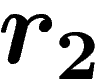 (except for
the trivial ``degenerate'' gluing between a polygon and the same one with
inverse orientation i.e.
(except for
the trivial ``degenerate'' gluing between a polygon and the same one with
inverse orientation i.e. 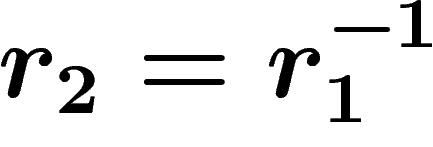 ).
).
If a group presentation satisfies the 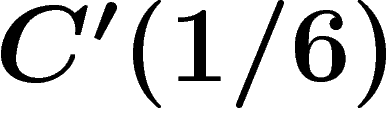 condition, then the group
is hyperbolic. This results from a simple Euler characteristic argument
on van Kampen diagrams, which allows to show that those have enough
boundary edges to ensure a linear isoperimetric inequality.
condition, then the group
is hyperbolic. This results from a simple Euler characteristic argument
on van Kampen diagrams, which allows to show that those have enough
boundary edges to ensure a linear isoperimetric inequality.
The limit case on which the significance of 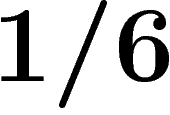 is clear is the
standard hexagonal tiling of the plane, which satisfies
is clear is the
standard hexagonal tiling of the plane, which satisfies 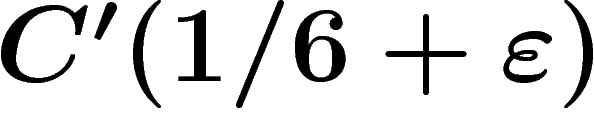 for any
for any 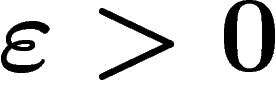 but not
but not 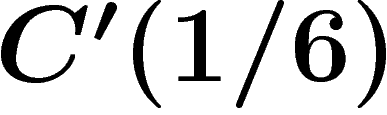 , and which is not hyperbolic (compare
the heptagonal tiling of the hyperbolic plane).
, and which is not hyperbolic (compare
the heptagonal tiling of the hyperbolic plane).
All in one: an example. Let G be the group presented by
![\[
\presgroup{a,b,c,d}{aba^{-1}b^{-1}cdc^{-1}d^{-1}=e}
\]](primer235.png)
![\includegraphics[scale=.75]{twocomms.eps}](primer236.png)
Now the only ways to glue such a polygon with a copy of itself consist in
gluing the two a's, or gluing the two b's, or the two c's, or the
two d's, but there is no way to find a gluing along two consecutive
letters. Since the length of the relator is 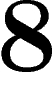 , this means that this
presentation satisfies the
, this means that this
presentation satisfies the 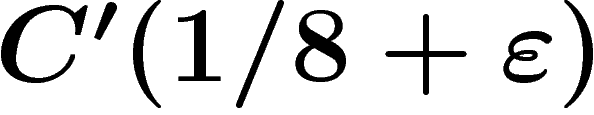 small cancellation condition
(but not
small cancellation condition
(but not 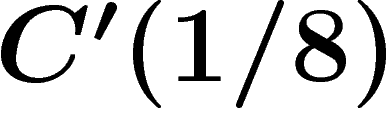 ). Since
). Since  the criterion above applies and so
this group is hyperbolic.
the criterion above applies and so
this group is hyperbolic.
This example is not anecdotic. Copies of the above octogon can be glued (in the allowed ways: an a with an a, etc.) to form the standard octogonal tiling of the hyperbolic plane. Actually this tiling is exactly the Cayley graph of the group, which we represent on the following figures in two different Euclidean views: a Poincaré model centered either on a face, emphasizing the tiling aspect, or on an element, emphasizing the Cayley graph. (When looking at the figures, keep in mind that the hyperbolic metric goes to infinity close to the disk boundary, so that all octogons are actually isometric and play the same role. The second picture is obtained from the first one by performing a hyperbolic isometry sending the left vertex of the large bottom a to the center of the disk.)
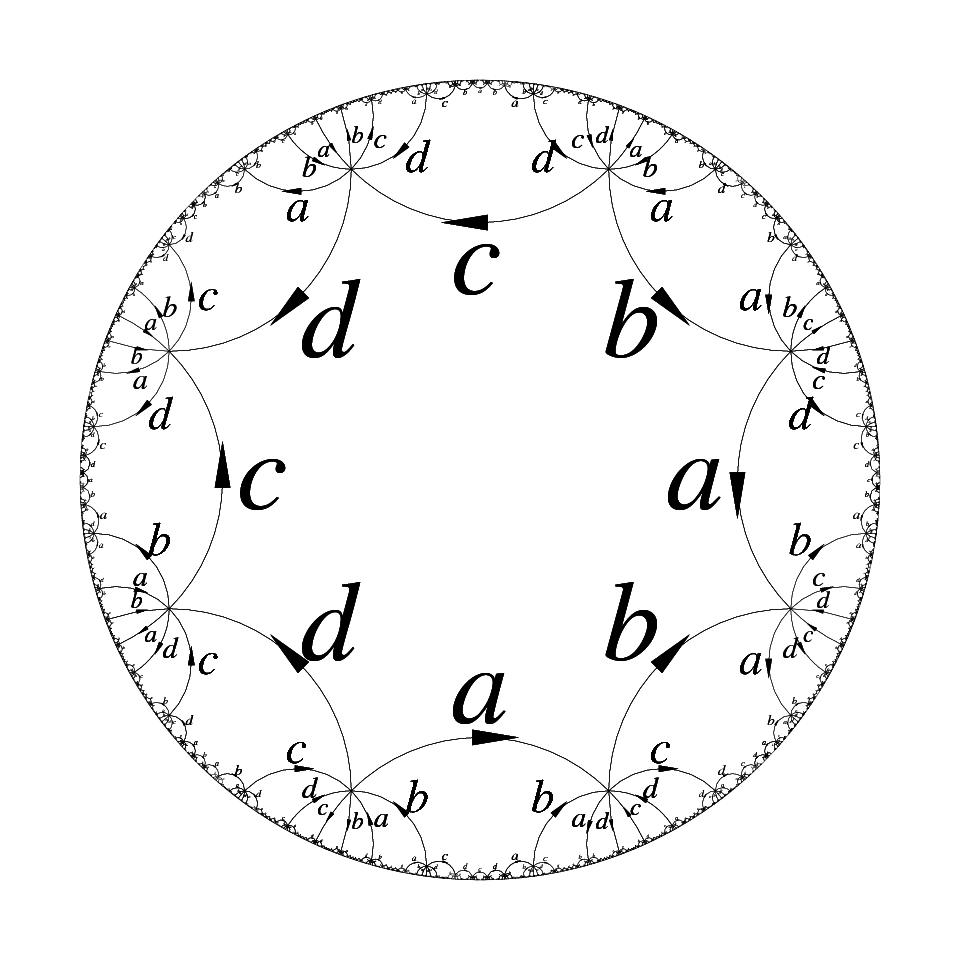
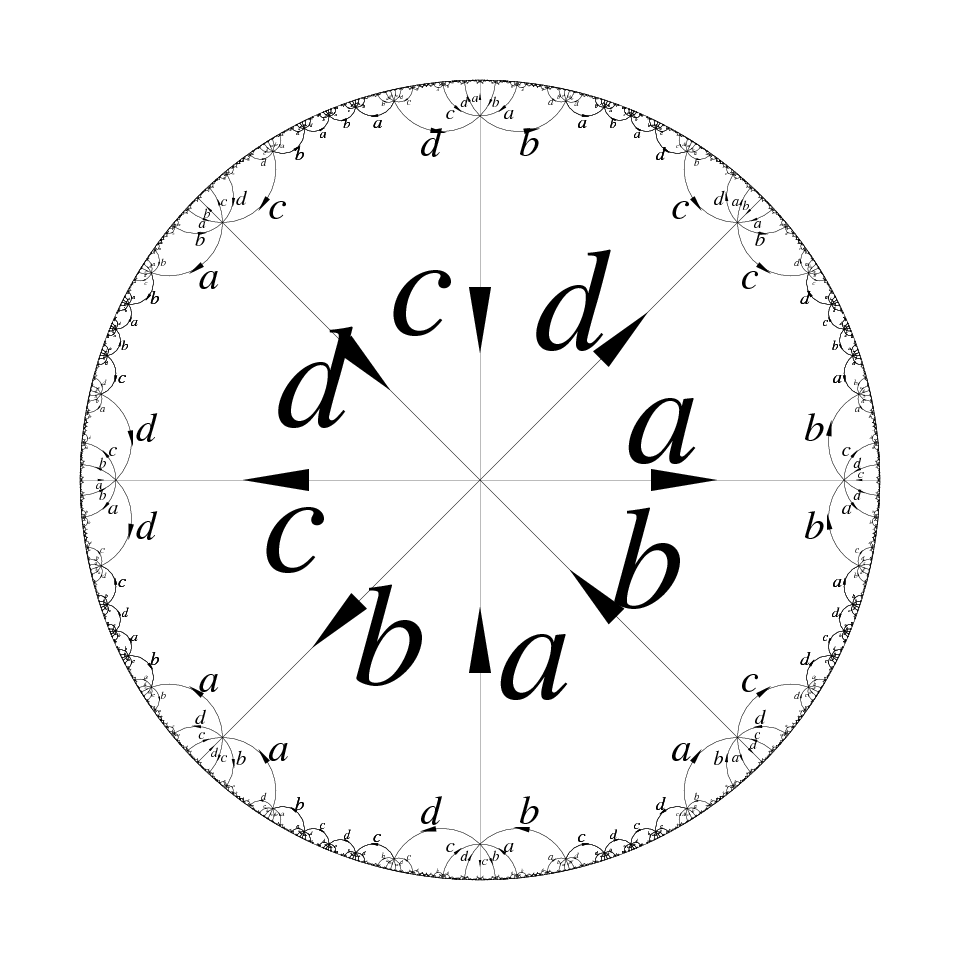
Since the hyperbolic plane is hyperbolic, this is another way to check hyperbolicity of this group: the group identifies with vertices of the tiling, equipped with the edge metric, which is a discrete subset quasi-isometric to the whole hyperbolic plane. Note how tree-like the Cayley graph looks in spite of the presence of cycles of length 8.
A group naturally acts on its Cayley graph by left multiplication and so we can take the quotient of this hyperbolic tiling by action of the group. This provides a two-dimensional object, the fundamental group of which is the group.
Let us take a closer look at this quotient. A single octogon is a
fundamental domain for the action of the group on the tiling (i.e. the
set of all translates of some octogon by the group exactly produces the
tiling) and so the quotient is obtained by taking a single octogon and
identifying its edges according to the labels. So take a single copy of
the octogon above and twist it in three-dimensional space so that the two
edges labelled by a are identified (preserving the orientation implied
by the arrows); then identify the two edges labelled by b, then the two
ones labelled by c, then the ones labelled by d (all eight vertices
will be identified along the way). This actually leaves
us with a surface of genus two, i.e. the gluing of two tori (this is
quite hard to figure out---check it first in the simpler case of a square
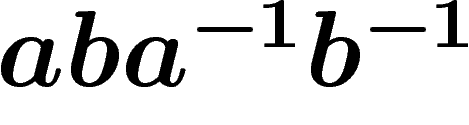 instead of the octogon above: this square transforms
into a torus).
instead of the octogon above: this square transforms
into a torus).
So the group can be represented as the fundamental group of a surface of
genus  . This surface inherits a metric of negative curvature from
that of the hyperbolic plane. Actually, fundamental groups of negatively
curved compact surfaces, or of polyhedra with negative curvature in some
combinatorial sense, were an important motivation for the introduction of
hyperbolic groups and initially the main source of examples.
. This surface inherits a metric of negative curvature from
that of the hyperbolic plane. Actually, fundamental groups of negatively
curved compact surfaces, or of polyhedra with negative curvature in some
combinatorial sense, were an important motivation for the introduction of
hyperbolic groups and initially the main source of examples.
Groups as geometric objects, hyperbolic groups, quasi-isometries,
Cayley graphs...
É. Ghys, P. de la Harpe, Sur les groupes
hyperboliques d'après Mikhael Gromov, Progress in Math. 83,
Birkhäuser (1990).
Groups as geometric objects, quasi-isometries...
M. Gromov, Infinite groups as geometric
objects, in Proceedings of the International Congress of
Mathematicians, Vol. 1, 2, Warsaw (1983), 385--392, PWN, Warsaw, 1984.
Group presentations, free groups, van Kampen diagrams (under the
name ``cancellation diagrams''), decision problems...
J. J. Rotman, An introduction to the theory
of groups, fourth edition, Graduate Texts in Mathematics 148,
Springer (1995), especially chapters 11 and 12.
Group presentations, free groups, van Kampen diagrams, small
cancellation theory...
R. C. Lyndon, P. E. Schupp, Combinatorial
group theory, Ergebnisse der Mathematik und ihrer
Grenzgebiete 89, Springer (1977).
Negative curvature, hyperbolic groups, isoperimetric
inequalities...
M. R. Bridson, A. Haefliger, Metric spaces of
non-positive curvature, Grundlehren der mathematischen
Wissenschaften 319, Springer (1999), especially chapters H
and  .
.