 des faisceaux. Notre but est
d'exposer la construction de base de
des faisceaux. Notre but est
d'exposer la construction de base de  dans différentes situations : la
définition d'objets cohomologiques globaux par recollement d'objets
définis sur les intersections des ouverts d'un recouvrement d'un espace.
dans différentes situations : la
définition d'objets cohomologiques globaux par recollement d'objets
définis sur les intersections des ouverts d'un recouvrement d'un espace.
Yann Ollivier, 10 mai 2001
Aussi au format pdf ou ps gzippé.
On définit ici la cohomologie de  des faisceaux. Notre but est
d'exposer la construction de base de
des faisceaux. Notre but est
d'exposer la construction de base de  dans différentes situations : la
définition d'objets cohomologiques globaux par recollement d'objets
définis sur les intersections des ouverts d'un recouvrement d'un espace.
dans différentes situations : la
définition d'objets cohomologiques globaux par recollement d'objets
définis sur les intersections des ouverts d'un recouvrement d'un espace.
On commence par motiver la construction de  en exposant le cas simple
des complexes. On utilise ensuite la cohomologie de
en exposant le cas simple
des complexes. On utilise ensuite la cohomologie de  des faisceaux
pour une démonstration particulièrement élégante du théorème de De Rham
(isomorphisme entre la cohomologie de De Rham et celle de
des faisceaux
pour une démonstration particulièrement élégante du théorème de De Rham
(isomorphisme entre la cohomologie de De Rham et celle de  à
coefficients dans
à
coefficients dans  pour une variété différentiable).
pour une variété différentiable).
Enfin, on donne une application de ces méthodes à l'étude des fibrés en droites (complexes), et on définit en particulier leur première classe de Chern. On démontre sur cette dernière une sorte de formule de Gauss-Bonnet.
Nous admettrons sans démonstration plusieurs théorèmes d'algèbre
homologique portant sur la cohomologie de  , qui peuvent se démontrer à
l'aide des techniques précédemment exposées dans le groupe de travail.
, qui peuvent se démontrer à
l'aide des techniques précédemment exposées dans le groupe de travail.
Une grande partie de l'exposé est une sélection du matériel des chapitres 0 et 1 de [GH].
 d'un complexe
d'un complexe
Un complexe combinatoire de sommets  est la
donnée d'un ensemble S de parties
de
est la
donnée d'un ensemble S de parties
de  , tel que
, tel que 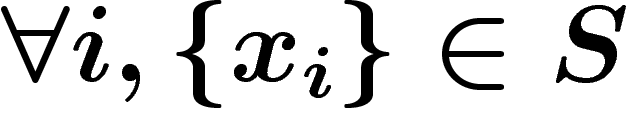 et tel que si
et tel que si  et
et  , alors
, alors  .
.
On peut se représenter un tel complexe dans  en plaçant
en plaçant 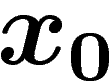 en
en
 , en plaçant les
, en plaçant les 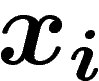 à distance 1 sur chacun des axes de
coordonnées, et en dessinant, pour tout
à distance 1 sur chacun des axes de
coordonnées, et en dessinant, pour tout 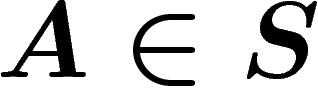 de cardinal i, un
simplexe de dimension
de cardinal i, un
simplexe de dimension 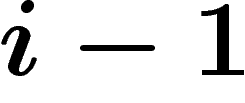 entre les sommets inclus dans A. La
condition dit alors que le bord d'un simplexe du complexe est dans le
complexe.
entre les sommets inclus dans A. La
condition dit alors que le bord d'un simplexe du complexe est dans le
complexe.
L'idée est de définir l'homologie de ce complexe de manière
combinatoire. Soit A un anneau, on note 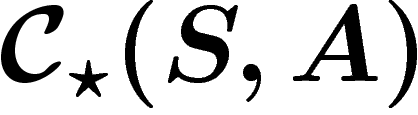 le module libre
le module libre
![$A[S]$](cech022.png) qu'on munit de la différentielle
qu'on munit de la différentielle
![\[
\d \left(x_{i_0},\ldots,x_{i_k}\right) =
\sum_{1\leq j\leq k} (-1)^j \left(
x_{i_0},\ldots,\widehat{x_{i_j}},\ldots,x_{i_k}\right)
\]](cech023.png)
On a ainsi défini un module différentiel gradué. Son homologie est
l'homologie de  du complexe combinatoire S.
du complexe combinatoire S.
On peut aussi définir la cohomologie, en notant 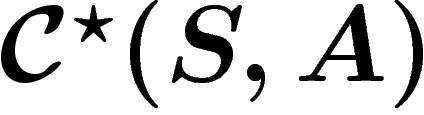 le
module des fonctions sur S à valeurs dans A (isomorphe au
précédent... nous sommes en dimension finie), et définir la
différentielle de
le
module des fonctions sur S à valeurs dans A (isomorphe au
précédent... nous sommes en dimension finie), et définir la
différentielle de 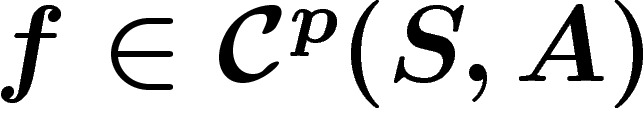 par
par 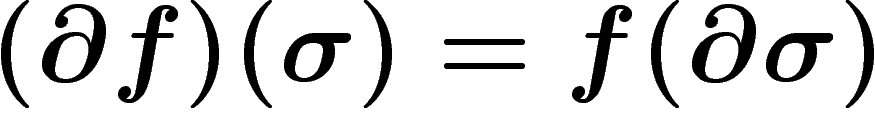 , ou
encore :
, ou
encore :
![\[
(\d f) \left(x_{i_0},\ldots,x_{i_k}\right) =
\sum_{1\leq j\leq k} (-1)^j f\left(
x_{i_0},\ldots,\widehat{x_{i_j}},\ldots,x_{i_k}\right)
\]](cech028.png)
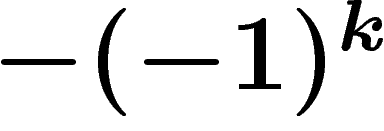 si l'on se préoccupe d'une belle
théorie de structures multiplicatives ensuite, ce qui ne sera pas notre
cas). La cohomologie de
si l'on se préoccupe d'une belle
théorie de structures multiplicatives ensuite, ce qui ne sera pas notre
cas). La cohomologie de  de S est alors la cohomologie de ce
complexe (elle est bien sûr isomorphe à l'homologie).
de S est alors la cohomologie de ce
complexe (elle est bien sûr isomorphe à l'homologie).
C'est ce point de vue combinatoire, où le bord d'un k-uplet est une
somme alternée de 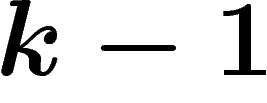 -uplets, qui définira la cohomologie de
-uplets, qui définira la cohomologie de  des
faisceaux. Un formalisme très similaire apparaît dans la
définition de la cohomologie des groupes. À noter que contrairement à la
théorie de l'homologie singulière, on ne manipule que des modules de
dimension finie.
des
faisceaux. Un formalisme très similaire apparaît dans la
définition de la cohomologie des groupes. À noter que contrairement à la
théorie de l'homologie singulière, on ne manipule que des modules de
dimension finie.
Telle que nous l'avons construite, l'homologie de  d'un complexe est
identique à l'homologie d'un dessin de ce complexe dans
d'un complexe est
identique à l'homologie d'un dessin de ce complexe dans 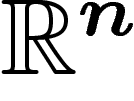 (ce n'est
pas immédiat).
(ce n'est
pas immédiat).
 des faisceaux
des faisceauxÀ l'origine de cette théorie, on trouve des problèmes de recollements. Si on a un recouvrement d'un espace topologique, si on a des fonctions définies sur chaque partie du recouvrement, et si ces fonctions se recollent bien sur chaque intersection de parties du recouvrement, alors on peut définir un objet global sur tout l'espace, qui sera un élément de la cohomologie de l'espace à valeurs dans notre espace de fonctions.
Par ailleurs, il peut être intéressant de regarder la cohomologie à
valeurs dans un espace qui pourrait varier d'un endroit à un autre. Si on
a par exemple un quotient Y d'un espace X : 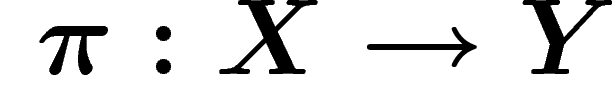 , on peut
vouloir obtenir des informations sur la cohomologie de X à partir de la
cohomologie de Y et, en tout point
, on peut
vouloir obtenir des informations sur la cohomologie de X à partir de la
cohomologie de Y et, en tout point 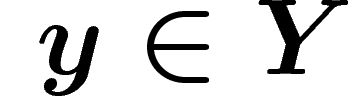 , de la cohomologie de la
fibre
, de la cohomologie de la
fibre 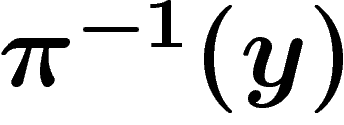 .
.
Ces considérations amènent à la définition des faisceaux, que nous rappelons.
Faisceaux.
Un faisceau  sur un espace topologique X est la donnée, pour
chaque ouvert U de X, d'un module
sur un espace topologique X est la donnée, pour
chaque ouvert U de X, d'un module 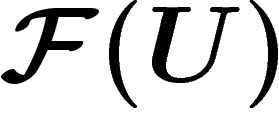 , dont les éléments sont
appelés sections au-dessus de U, ainsi que d'un morphisme de
restriction d'un ouvert à un autre
, dont les éléments sont
appelés sections au-dessus de U, ainsi que d'un morphisme de
restriction d'un ouvert à un autre 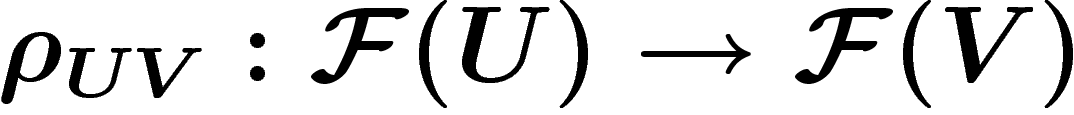 , pour
, pour
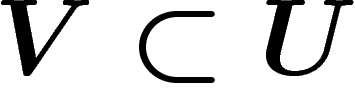 . On demande les conditions suivantes pour tous ouverts U,
V, W, qui expriment que ce
cette restriction ressemble à ce qu'on appelle usuellement restriction :
. On demande les conditions suivantes pour tous ouverts U,
V, W, qui expriment que ce
cette restriction ressemble à ce qu'on appelle usuellement restriction :
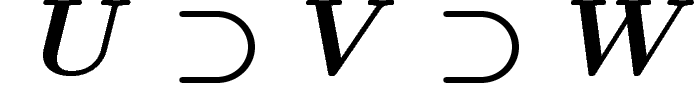 , alors
, alors 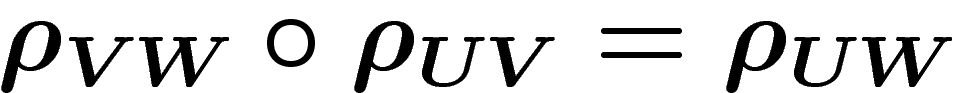 .
.
 sont égales, alors il existe une section sur
sont égales, alors il existe une section sur
 qui se restreint à celles-là sur U et V.
qui se restreint à celles-là sur U et V.
 sont
toutes deux nulles, alors cette section est nulle.
sont
toutes deux nulles, alors cette section est nulle.
On notera indifféremment 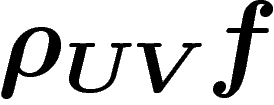 ou
ou 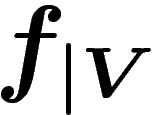 .
.
Par exemple, l'espace des fonctions continues sur les ouverts d'un espace topologique est un faisceau.
Un autre faisceau que nous utiliserons par
la suite est celui des fonctions localement constantes à valeurs dans
 ou
ou 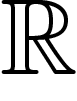 . Étudier les conditions de recollement de fonctions
localement constantes revient exactement à étudier l'homologie usuelle de
l'espace (cf. ci-dessous).
. Étudier les conditions de recollement de fonctions
localement constantes revient exactement à étudier l'homologie usuelle de
l'espace (cf. ci-dessous).
Un morphisme de faisceaux 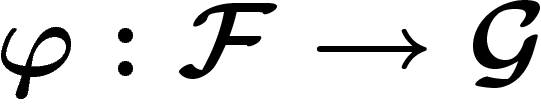 est simplement une collection
de morphismes
est simplement une collection
de morphismes 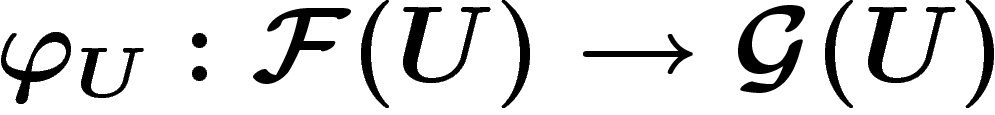 pour tout ouvert U, commutant à
la restriction.
pour tout ouvert U, commutant à
la restriction.
Le noyau d'un morphisme de faisceaux est un sous-faisceau du faisceau de départ, défini sur chaque ouvert comme le noyau du morphisme sur cet ouvert. C'est bien un faisceau.
Quotients de faisceaux. Pour définir un quotient de faisceaux, il n'est pas correct de prendre au-dessus de chaque ouvert le quotient correspondant : cela ne donne pas toujours un faisceau.
Par exemple, si l'on prend, sur l'espace 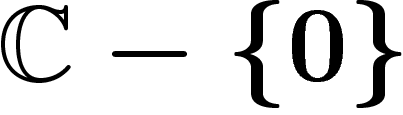 , la fonction
exponentielle
, la fonction
exponentielle 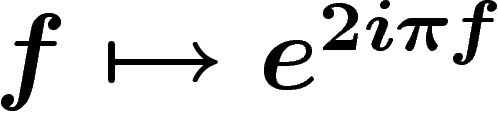 qui est un morphisme du faisceau des
fonctions holomorphes vers celui des fonctions holomorphes ne s'annulant
pas sur
qui est un morphisme du faisceau des
fonctions holomorphes vers celui des fonctions holomorphes ne s'annulant
pas sur 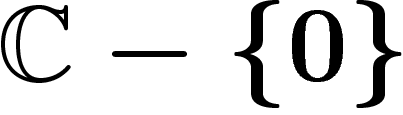 , on voit que la fonction z n'est pas
dans l'image, tandis que sa restriction à tout ouvert de
, on voit que la fonction z n'est pas
dans l'image, tandis que sa restriction à tout ouvert de 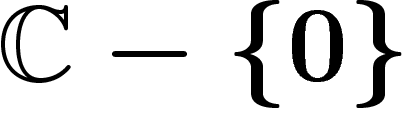 n'entourant pas l'origine y est (on peut en prendre le logarithme), ce
qui contredit la propriété de recollement des faisceaux.
n'entourant pas l'origine y est (on peut en prendre le logarithme), ce
qui contredit la propriété de recollement des faisceaux.
On voudrait donc dire qu'une section appartient à l'image d'un morphisme de faisceaux si on peut trouver un découpage de son support en ouverts plus petits, tel que sur chacun de ces ouverts, sa restriction soit effectivement atteinte. Ceci amène la définition suivante.
Le faisceau quotient du faisceau  par le sous-faisceau
par le sous-faisceau
 est le faisceau dont une section
est le faisceau dont une section  au-dessus d'un
ouvert U est donnée par un recouvrement ouvert
au-dessus d'un
ouvert U est donnée par un recouvrement ouvert 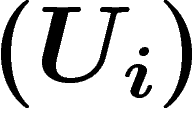 de
U et une famille de sections
de
U et une famille de sections  coïncidant sur les
intersections :
coïncidant sur les
intersections : 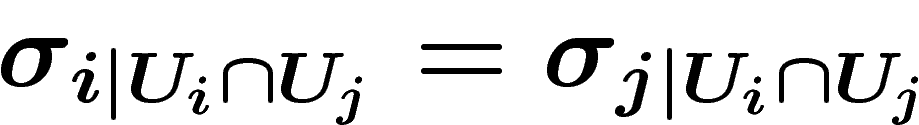 ; deux
telles sections
; deux
telles sections 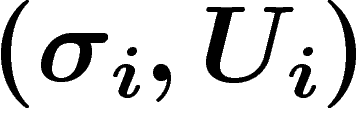 et
et 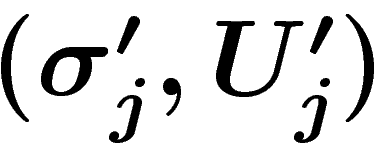 sont identifiées
si leur différence est localement dans
sont identifiées
si leur différence est localement dans  , i.e. si en tout point
, i.e. si en tout point 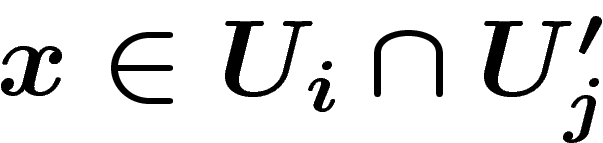 , on peut trouver un voisinage V de x tel que
, on peut trouver un voisinage V de x tel que
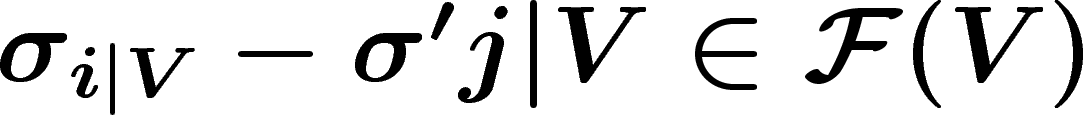 .
.
Une suite de morphismes de faisceaux
![\[
0\ra \F \stackrel{\phi}{\ra} \G \stackrel{\psi}{\ra} \H \ra 0
\]](cech069.png)
 fait de
fait de  un sous-faisceau de
un sous-faisceau de  et si
et si
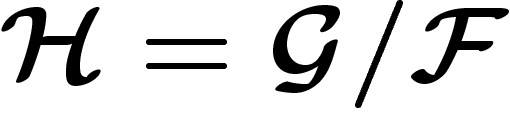 par
par  .
.
Une suite de faisceaux
![\[
\cdots \ra \F_n \stackrel{\phi_n}{\lra} \F_{n+1} \stackrel{\phi_{n+1}}{\lra}
\F_{n+2} \ra \cdots
\]](cech075.png)
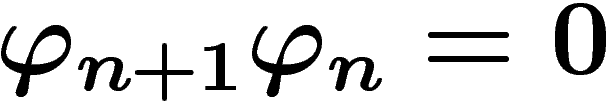 et si
et si
 .
.
En conclusion, si  est exacte, il est faux
de dire que
est exacte, il est faux
de dire que 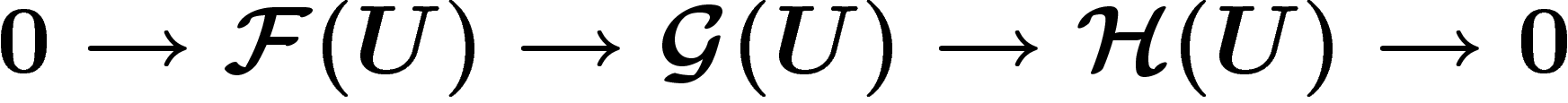 le soit aussi pour un
ouvert U : la dernière flèche n'est que localement surjective.
le soit aussi pour un
ouvert U : la dernière flèche n'est que localement surjective.

La cohomologie de  à valeurs dans un faisceau représente l'obstruction
au recollement de solutions locales dans le faisceau, en une solution
globale. On étudie un exemple d'où sort naturellement le formalisme de
à valeurs dans un faisceau représente l'obstruction
au recollement de solutions locales dans le faisceau, en une solution
globale. On étudie un exemple d'où sort naturellement le formalisme de
 .
.
Exemple. Soit le problème de Mittag-Leffler : sur une variété
complexe, trouver une fonction méromorphe ayant des pôles prescrits, et
holomorphe ailleurs. Localement (dans un ouvert  contenant un seul
pôle prescrit), le problème est trivial. Soit donc
contenant un seul
pôle prescrit), le problème est trivial. Soit donc 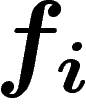 une solution
méromorphe au-dessus de
une solution
méromorphe au-dessus de 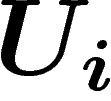 .
.
On veut trouver une fonction globale f telle que sur chaque 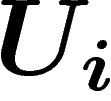 ,
,
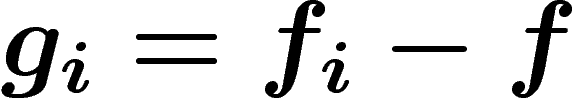 soit holomorphe. Il est donc nécessaire et suffisant de
trouver des
soit holomorphe. Il est donc nécessaire et suffisant de
trouver des 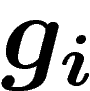 holomorphes et se recollant bien i.e. sur
holomorphes et se recollant bien i.e. sur  ,
, 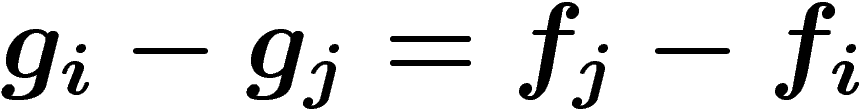 . Si l'on introduit les
. Si l'on introduit les
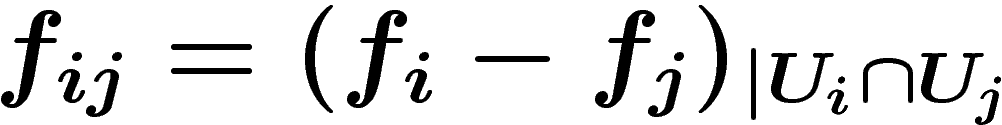 , le problème revient à écrire les
, le problème revient à écrire les
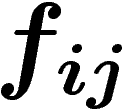 définis sur chaque intersection d'ouverts, comme différence de
fonctions définies sur ces ouverts. On dira alors que les
définis sur chaque intersection d'ouverts, comme différence de
fonctions définies sur ces ouverts. On dira alors que les 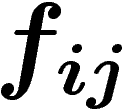 sont un
(co)bord.
sont un
(co)bord.
Cependant, les 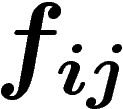 ne sont pas tout à fait quelconques : ce sont des
différences de fonctions (méromorphes, pas holomorphes comme on le
souhaiterait) sur
ne sont pas tout à fait quelconques : ce sont des
différences de fonctions (méromorphes, pas holomorphes comme on le
souhaiterait) sur 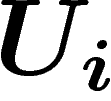 et
et 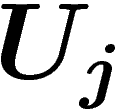 . Elles vérifient, en particulier, la
relation
. Elles vérifient, en particulier, la
relation 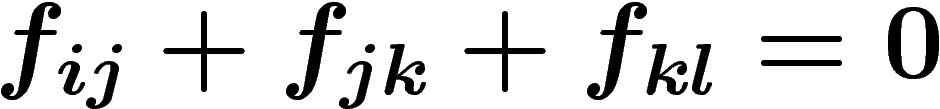 . On dit qu'elles forment un (co)cycle. Au
final la question est d'écrire un (co)cycle comme un (co)bord.
. On dit qu'elles forment un (co)cycle. Au
final la question est d'écrire un (co)cycle comme un (co)bord.
Cohomologie de  . Soit X un espace topologique muni d'un
faisceau
. Soit X un espace topologique muni d'un
faisceau  . Soit
. Soit 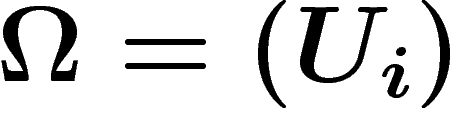 un recouvrement ouvert de
X. On définit les cochaînes de degré k à valeurs dans
un recouvrement ouvert de
X. On définit les cochaînes de degré k à valeurs dans  comme les
applications qui à chaque k-uplet d'ouverts du recouvrement, associent
une section sur leur intersection :
comme les
applications qui à chaque k-uplet d'ouverts du recouvrement, associent
une section sur leur intersection :
![\[
C^k(\Omega,\F)=\prod_{i_0, \ldots, i_k}
\F(U_{i_0}\cap\ldots \cap U_{i_k})
\]](cech102.png)
On définit l'opérateur bord 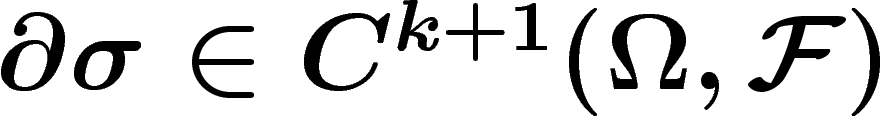 pour
pour
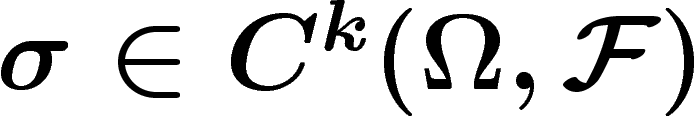 par
par
![\[
\d \sigma(U_{i_0},\ldots,U_{i_{k+1}})=\sum_{j=0}^{k+1}
(-1)^j\sigma(U_{i_0},\ldots,\widehat{U_{i_j}},\ldots,U_{i_{k+1}})_{|U_{i_0}\cap\ldots\cap
U_{i_{k+1}}}
\]](cech105.png)
Écrivons pour l'exercice, cette définition en degré 0 et 1 :
![\[(\d \sigma_0)(U,V)=\sigma_0(V)-\sigma_0(U)\]](cech106.png)
![\[(\d \sigma_1)(U,V,W)=\sigma_1(V,W)-\sigma_1(U,W)+\sigma_1(V,W)\]](cech107.png)
La cohomologie de  du faisceau
du faisceau  pour le recouvrement
pour le recouvrement  est
la cohomologie de ce complexe :
est
la cohomologie de ce complexe :
![\[
H^k(U,\F)=\frac{\Ker \d : C^k(U,\F) \ra C^{k+1}(U,\F)}{\Img \d :
C^{k-1}(U,\F) \ra C^k(U,\F)}
\]](cech111.png)
Tout ceci dépend de notre choix de recouvrement. On a évidemment une application naturelle de la cohomologie sur un recouvrement vers la cohomologie sur un recouvrement plus fin. Ceci permet de définir rondement la cohomologie de v{C}ech de l'espace X comme la limite inductive, sur tous les recouvrements, de la cohomologie ci-dessus :
![\[
H^\ast(X,\F)=\ilim{\Omega}H^\ast(\Omega,\F)
\]](cech112.png)
D'abord, 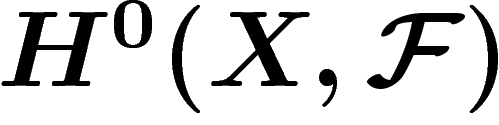 n'est autre que l'ensemble des sections globales de
X dans
n'est autre que l'ensemble des sections globales de
X dans  (ce sont des sections définies sur les ouverts qui
coïncident sur leur intersection). Ceci montre que la cohomologie de
(ce sont des sections définies sur les ouverts qui
coïncident sur leur intersection). Ceci montre que la cohomologie de  contient autant d'information sur le faisceau que sur l'espace
sous-jacent.
contient autant d'information sur le faisceau que sur l'espace
sous-jacent.
La cohomologie de  des faisceaux est covariante en le faisceau
d'arrivée : un morphisme de faisceaux définit naturellement un morphisme
en cohomologie à coefficients dans ces faisceaux.
des faisceaux est covariante en le faisceau
d'arrivée : un morphisme de faisceaux définit naturellement un morphisme
en cohomologie à coefficients dans ces faisceaux.
Notons que tout cocycle doit vérifier la condition d'antisymétrie
![\[
\sigma(U_0,\ldots,U_i,U_{i+1},\ldots,U_p)=-\sigma(U_0,\ldots,U_{i+1},U_i,\ldots,U_p).
\]](cech117.png)
En prenant comme faisceau les fonctions localement constantes à
valeurs dans  , si sur un le dessin d'un complexe combinatoire on
prend comme recouvrement ouvert les sommets, faces et arêtes un peu
épaissis, on voit qu'on obtient exactement la cohomologie de
, si sur un le dessin d'un complexe combinatoire on
prend comme recouvrement ouvert les sommets, faces et arêtes un peu
épaissis, on voit qu'on obtient exactement la cohomologie de  du
complexe combinatoire. On admettra que sur toute variété, la cohomologie
de
du
complexe combinatoire. On admettra que sur toute variété, la cohomologie
de  à coefficients dans
à coefficients dans  est isomorphe à la cohomologie
singulière.
est isomorphe à la cohomologie
singulière.
Par ailleurs, toute suite exacte de faisceaux  définit une suite exacte longue en cohomologie
définit une suite exacte longue en cohomologie
![\[
\begin{array}{ccccccc}
0 & \ra & H^0(X,\F) & \ra & H^0(X,\G) & \ra & H^0(X,\H) \\
& \stackrel{\d}{\ra} & H^1(X,\F) & \ra & H^1(X,\G) & \ra &
H^1(X,\H)\ldots\\
& & & & \vdots \\
& \stackrel{\d}{\ra} & H^p(X,\F) & \ra & H^p(X,\G) & \ra &
H^p(X,\H)\ldots
\end{array}
\]](cech123.png)
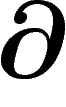 s'obtient en remarquant que si un élément de
s'obtient en remarquant que si un élément de
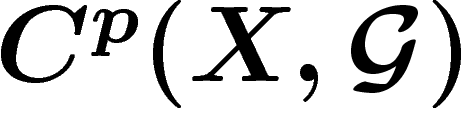 , vu dans
, vu dans 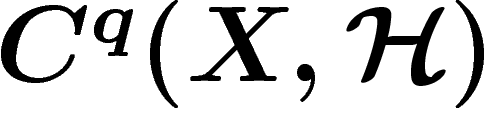 , est de bord nul, c'est que son bord est
dans
, est de bord nul, c'est que son bord est
dans 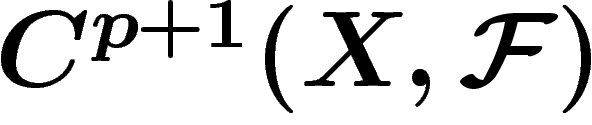 . La vérification de l'exactitude est pénible à cause de la limite sur les recouvrements et de
la définition locale des suites exactes de faisceaux.
. La vérification de l'exactitude est pénible à cause de la limite sur les recouvrements et de
la définition locale des suites exactes de faisceaux.
Cette suite exacte permet de résoudre, au moins théoriquement, les
problèmes de surjectivité globale. Si  est
une suite exacte de faisceaux, si
est
une suite exacte de faisceaux, si  est une section globale
de
est une section globale
de 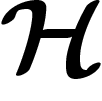 , x est l'image d'une section globale de
, x est l'image d'une section globale de  si et seulement si
si et seulement si
 est nul dans
est nul dans 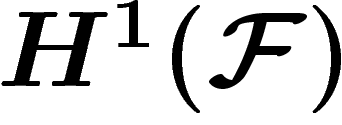 .
.
La vérification de la suite exacte de Mayer-Vietoris pour une partition en deux ouverts est assez simple.
Le problème du passage à la limite peut être contourné quand on
connaît le théorème de Leray, qui affirme que si les ouverts 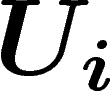 d'un
recouvrement sont tels que
d'un
recouvrement sont tels que 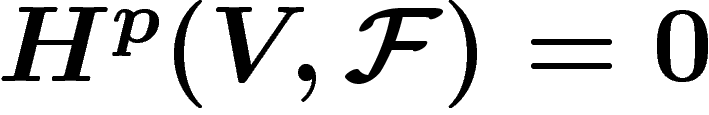 pour
pour 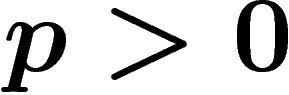 et pour toute
intersection finie V des
et pour toute
intersection finie V des 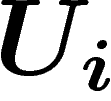 , alors la cohomologie de
, alors la cohomologie de  du
recouvrement est identique à la limite. Ce théorème se démontre à l'aide
d'outils d'algèbre homologique n'ayant pas leur place ici (cf. [G]).
C'est ce théorème qui rend calculables les cohomologies d'un grand nombre
de faisceaux.
du
recouvrement est identique à la limite. Ce théorème se démontre à l'aide
d'outils d'algèbre homologique n'ayant pas leur place ici (cf. [G]).
C'est ce théorème qui rend calculables les cohomologies d'un grand nombre
de faisceaux.
Enfin, mentionnons une dernière propriété : si l'on se place sur une
variété M, le faisceau des fonctions 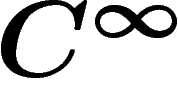 sur M admet des
partitions de l'unité. On peut alors voir que sa cohomologie en degré
strictement positif est nulle. En effet, soit
sur M admet des
partitions de l'unité. On peut alors voir que sa cohomologie en degré
strictement positif est nulle. En effet, soit 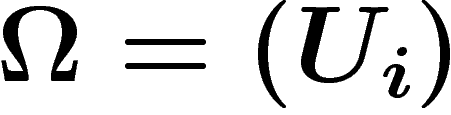 un
recouvrement ouvert de M, soit
un
recouvrement ouvert de M, soit 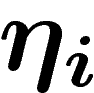 une partition de l'unité y
subordonnée, et soit
une partition de l'unité y
subordonnée, et soit 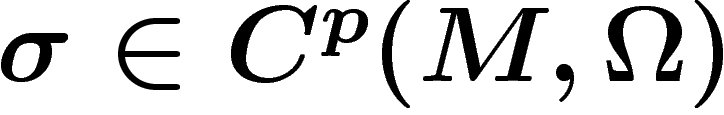 un cocycle. On pose
un cocycle. On pose
![\[
\tau(U_{i_0},\ldots,U_{i_{p-1}})=\sum_j \rho_j
\sigma(U_j,U_{i_0},\ldots,U_{i_{p-1}}) \]](cech143.png)
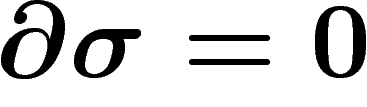 , que
, que 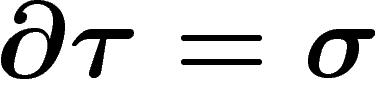 . Plus généralement, il
en sera de même de tout faisceau en
. Plus généralement, il
en sera de même de tout faisceau en 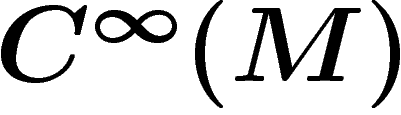 -modules, en multipliant
de la même manière par des partitions de l'unité
-modules, en multipliant
de la même manière par des partitions de l'unité 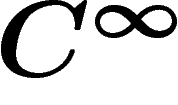 . En
particulier, le faisceau
. En
particulier, le faisceau 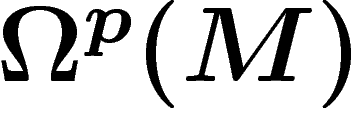 des p-formes différentielles
vérifie
des p-formes différentielles
vérifie 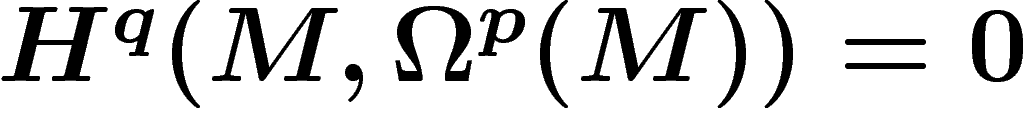 pour
pour 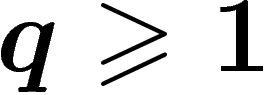 .
.
Nous montrons ici que la cohomologie de De Rham d'une variété est
isomorphe à sa cohomologie de  à coefficients dans
à coefficients dans 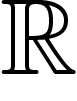 .
.
L'argument, très court, utilise des suites exactes de faisceaux. En fait,
il revient à faire passer, degré par degré, le côté « on intègre autour
d'un trou » de la cohomologie de De Rham en un recouvrement construit
autour du trou, dans l'idée combinatoire de  , en montrant que chaque
étape est un isomorphisme.
, en montrant que chaque
étape est un isomorphisme.
Soit M une variété, soit 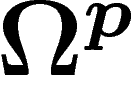 le faisceau des p-formes
différentielles sur M, et soit
le faisceau des p-formes
différentielles sur M, et soit 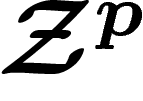 celui des p-formes fermées.
celui des p-formes fermées.
La cohomologie de De Rham en degré p est le quotient des p-formes
fermées par les différentielles des 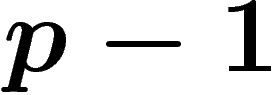 -formes. Une p-forme est, par
définition, une section globale du faisceau des p-formes (!!!!), donc un
élément de
-formes. Une p-forme est, par
définition, une section globale du faisceau des p-formes (!!!!), donc un
élément de 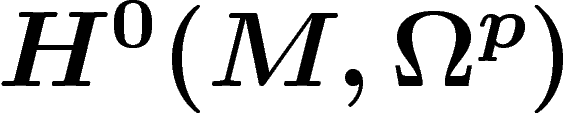 puisque le
puisque le  s'identifie aux sections
globales. D'où :
s'identifie aux sections
globales. D'où :
![\[
H_{DR}^p(M)=\frac{H^0(M,\Zz^p)}{d_\ast H^0(M,\Omega^{p-1})}
\]](cech159.png)
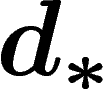 désigne l'application en cohomologie associée à
l'application
désigne l'application en cohomologie associée à
l'application 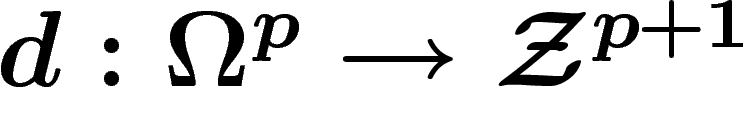 .
.
D'après le lemme de Poincaré, toute forme fermée est localement exacte, et donc les suites de faisceaux
![\[
0\ra \Zz^p \ra \Omega^p \stackrel{d}{\ra} \Zz^{p+1} \ra 0
\]](cech162.png)
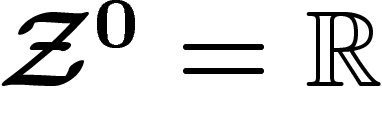 , faisceau des fonctions
localement constantes, et
, faisceau des fonctions
localement constantes, et 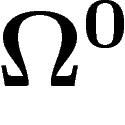 le faisceau des fonctions
le faisceau des fonctions 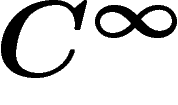 ).
).
Écrivons donc partiellement les suites exactes longues en cohomologie associées à ces suites exactes de faisceaux :
![\[
H^q(M,\Omega^p) \stackrel{d_\ast}{\ra} H^q(M,\Zz^{p+1}) \stackrel{\d}{\ra}
H^{q+1}(M,\Zz^p) \ra H^{q+1}(M,\Omega^p)
\]](cech166.png)
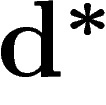 est la différentielle
extérieure et
est la différentielle
extérieure et 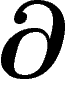 l'opérateur bord de la longue suite exacte.
l'opérateur bord de la longue suite exacte.
Or le faisceau 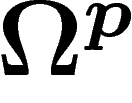 admet des partitions de l'unité, donc
admet des partitions de l'unité, donc
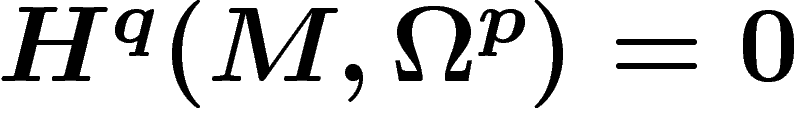 pour
pour 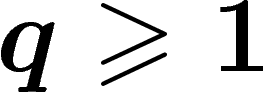 et par conséquent
et par conséquent
![\[
H^q(M,\Zz^{p+1})=H^{q+1}(M,\Zz^p)
\]](cech172.png)
Pour 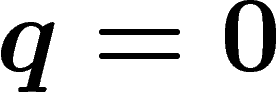 , on obtient
, on obtient
![\[
H^0(M,\Omega^p) \stackrel{\mathrm{d}^\ast}{\ra} H^0(M,\Zz^{p+1})
\stackrel{\d}{\ra} H^1(M,\Zz^p)\ra 0
\]](cech174.png)
![\[
H^1(M,\Zz^p)=\frac{H^0(M,\Zz^{p+1})}{\mathrm{d}^\ast H^0(M,\Omega^p)}
\]](cech175.png)
On a donc
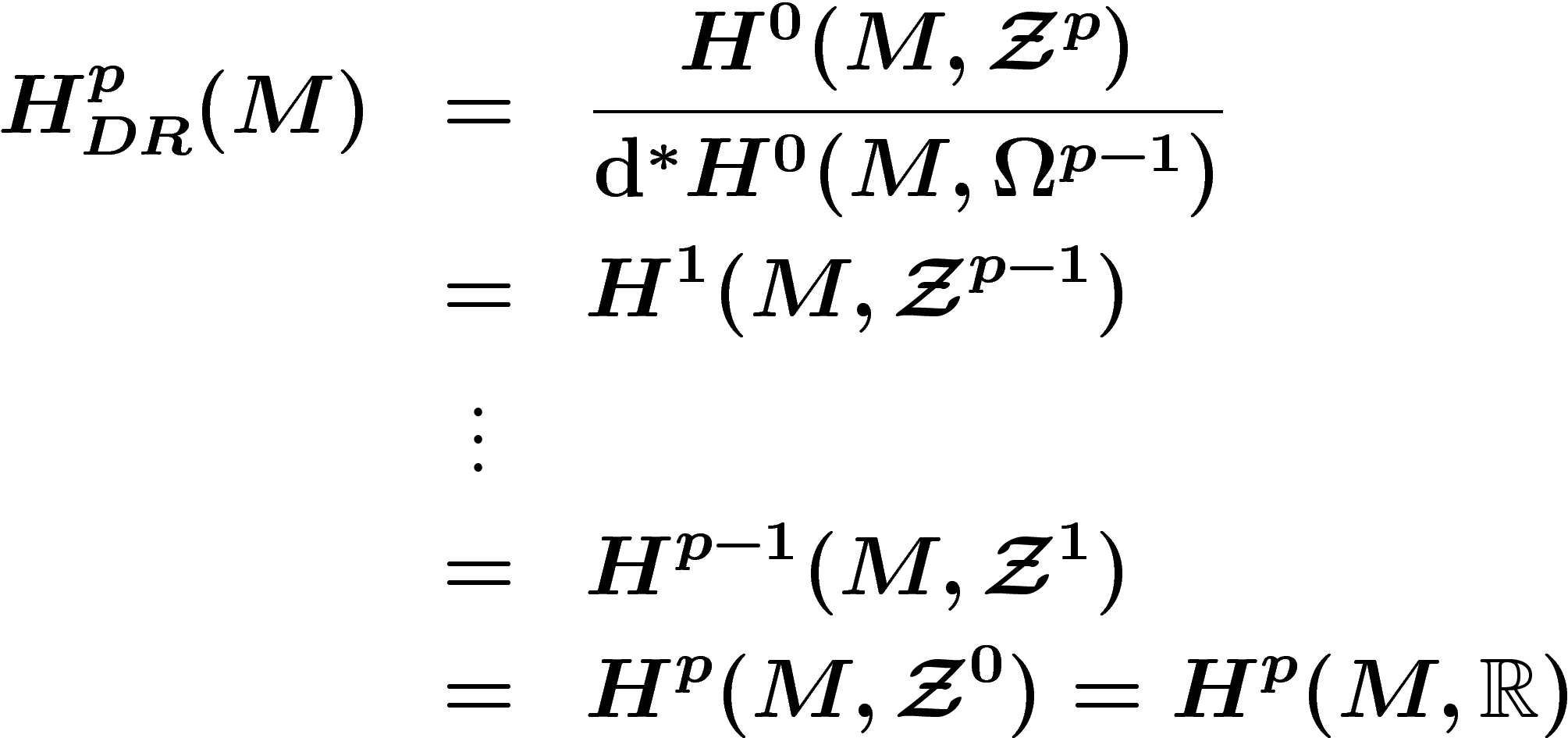
On s'intéresse désormais à des fibrés en droites réelles ou complexes, et
on montre comment la cohomologie de  contribue à leur classification.
En particulier, on définira la première classe de Chern d'un fibré en
droites complexes et on démontrera qu'elle
s'identifie à la forme de courbure de ce fibré, ce qui constitue une
sorte de formule de Gauss-Bonnet.
contribue à leur classification.
En particulier, on définira la première classe de Chern d'un fibré en
droites complexes et on démontrera qu'elle
s'identifie à la forme de courbure de ce fibré, ce qui constitue une
sorte de formule de Gauss-Bonnet.
(Les variétés ainsi que toutes les applications mentionnées dans ce
paragraphe sont 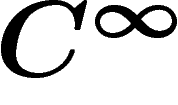 ).
).
Le point de départ est l'intuition que la seule non-trivialité qui puisse
arriver à un fibré en droites réelles est de faire un tour sur lui-même
quand on suit un lacet non trivial dans la variété de base. On voudrait
donc dire que l'ensemble des fibrés en droites sur une variété M
ressemble à 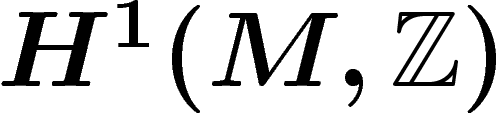 ou
ou 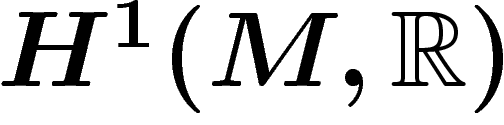
Ceci n'est pas tout à fait vrai. Si par exemple sur le cercle, on prend
une droite qui fait deux tours sur elle-même, le fibré obtenu est
isomorphe au fibré trivial. Deux tours semblent donc ne compter
pour rien. Notre nouvelle conjecture est donc que l'ensemble des fibrés
en droite s'identifie à 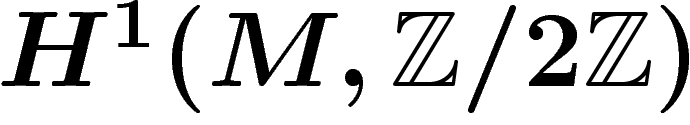 .
.
Un petit détour par  , qui est l'exemple le plus simple où
on voit bien apparaître les coefficients dans
, qui est l'exemple le plus simple où
on voit bien apparaître les coefficients dans
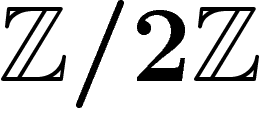 , semble montrer que cette conjecture tient la route : il existe
un fibré en droites qui fait exactement un tour sur lui-même lorsqu'on
parcourt une droite de
, semble montrer que cette conjecture tient la route : il existe
un fibré en droites qui fait exactement un tour sur lui-même lorsqu'on
parcourt une droite de  de
de  à
à  (par
exemple, si la droite est horizontale, prendre le fibré engendré par la
direction verticale en chaque point). Nous allons montrer qu'en effet,
cette conjecture est exacte.
(par
exemple, si la droite est horizontale, prendre le fibré engendré par la
direction verticale en chaque point). Nous allons montrer qu'en effet,
cette conjecture est exacte.
Un fibré vectoriel sur une variété M est la donnée d'une
variété E, d'une projection 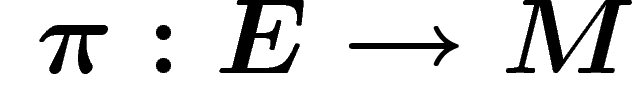 telle que
telle que 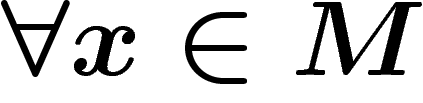 ,
,
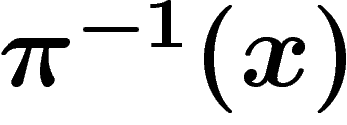 est muni d'une structure d'espace vectoriel isomorphe à un
espace vectoriel F, et d'un recouvrement ouvert
est muni d'une structure d'espace vectoriel isomorphe à un
espace vectoriel F, et d'un recouvrement ouvert 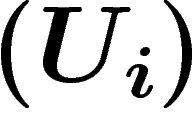 de M avec des
cartes
de M avec des
cartes 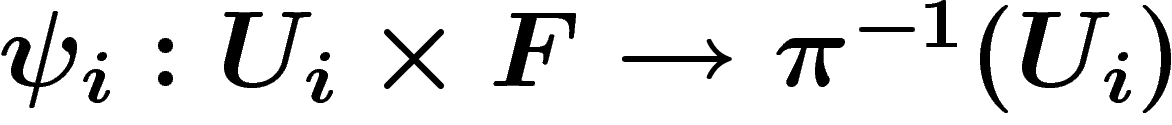 telles que d'une part,
telles que d'une part,
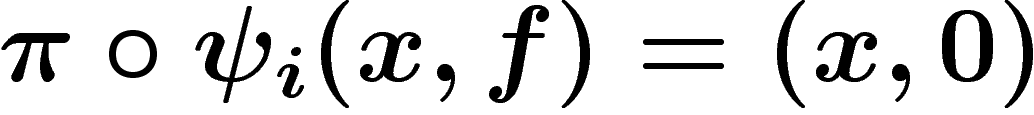 , et d'autre part sur
, et d'autre part sur  ,
,
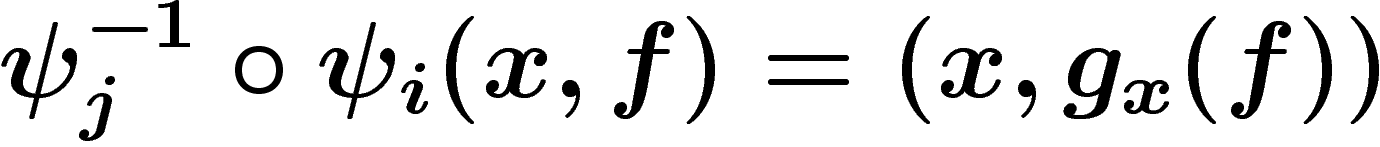 où
où 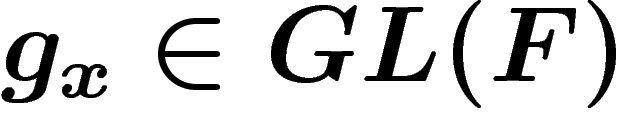 .
.
On demande donc que localement le fibré soit simplement un produit de la
variété par un espace vectoriel, et que ces produits locaux se recollent
globalement, ce qui est dans l'esprit même de la cohomologie de  .
.
On prend désormais 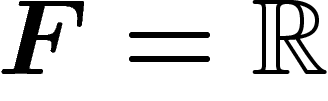 car, pour pousser l'analogie, il est beaucoup
plus commode que
car, pour pousser l'analogie, il est beaucoup
plus commode que 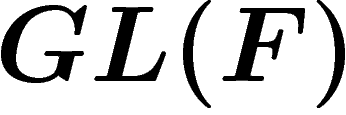 soit commutatif.
soit commutatif.
Plus précisément, donc, si on a un fibré en droites réelles, si 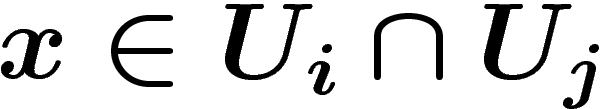 appelons
appelons 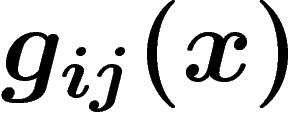 l'élément
l'élément 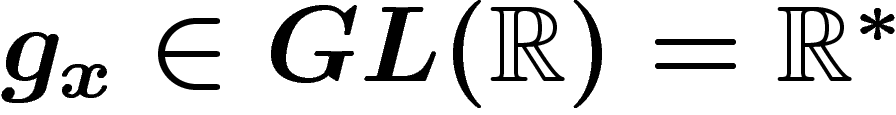 précédemment défini. Alors g est simplement une cochaîne de
précédemment défini. Alors g est simplement une cochaîne de  de
degré 1 (définie sur les intersections d'ouverts du recouvrement) à
valeurs dans le faisceau (multiplicatif) des fonctions
de
degré 1 (définie sur les intersections d'ouverts du recouvrement) à
valeurs dans le faisceau (multiplicatif) des fonctions 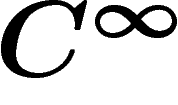 de M
dans
de M
dans 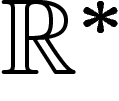 .
.
Et même, sur les intersections de trois ouverts 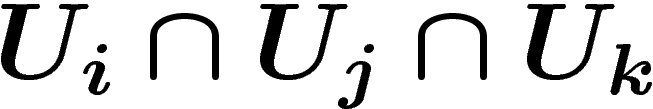 , on
a bien sûr
, on
a bien sûr 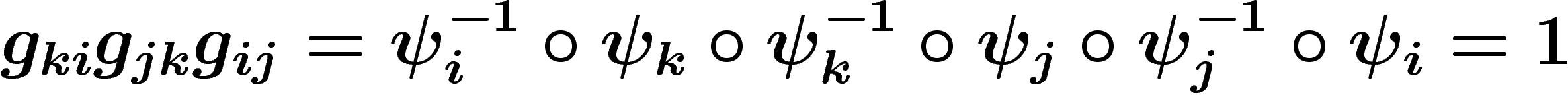 . Cela signifie
que les
. Cela signifie
que les 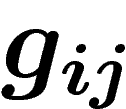 forment un cocycle de
forment un cocycle de  .
.
Inversement, étant données des fonctions 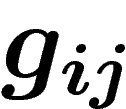 de chaque
de chaque  dans
dans 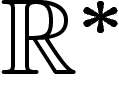 vérifiant ces conditions, on peut construire un fibré en
prenant d'abord l'union disjointe des
vérifiant ces conditions, on peut construire un fibré en
prenant d'abord l'union disjointe des  , puis en identifiant
les points au-dessus de
, puis en identifiant
les points au-dessus de  selon les
selon les 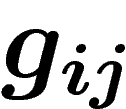 . La relation de
cocycle dit alors exactement que cette identification est une relation
d'équivalence.
. La relation de
cocycle dit alors exactement que cette identification est une relation
d'équivalence.
Montrons que le fibré défini par un cocycle ne dépend que de
sa classe d'homologie. Si 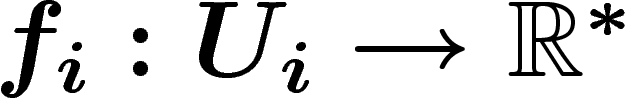 est une 0-chaîne,
ajouter son bord à une 1-chaîne
est une 0-chaîne,
ajouter son bord à une 1-chaîne 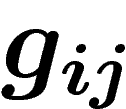 la transforme en
la transforme en
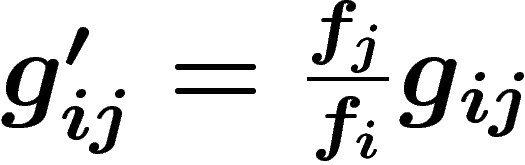 . Le fibré défini par cette nouvelle
2-chaîne est isomorphe à celui de départ : on a seulement changé chaque
carte
. Le fibré défini par cette nouvelle
2-chaîne est isomorphe à celui de départ : on a seulement changé chaque
carte  en
en  par multiplication par
par multiplication par 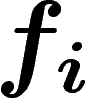 .
Inversement, toute autre trivialisation du même fibré est obtenue par
application, pour chaque
.
Inversement, toute autre trivialisation du même fibré est obtenue par
application, pour chaque 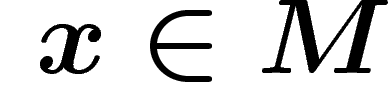 , d'un élément
, d'un élément 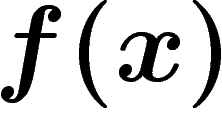 de
de 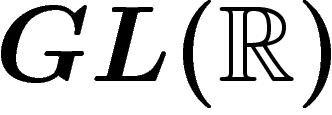 , et la
restriction à chaque
, et la
restriction à chaque 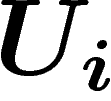 de f définit une 0-chaîne dont on devra
ajouter le bord aux
de f définit une 0-chaîne dont on devra
ajouter le bord aux 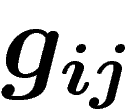 pour obtenir la nouvelle trivialisation.
pour obtenir la nouvelle trivialisation.
Ainsi, l'ensemble des fibrés en droites sur M s'identifie à 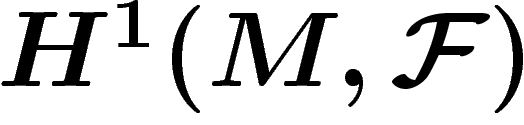 où
où  est le faisceau multiplicatif des fonctions
est le faisceau multiplicatif des fonctions 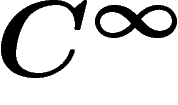 réelles ne
s'annulant pas sur M. La structure algébrique est préservée : le
produit tensoriel des fibrés en droites est la somme (plutôt multiplication)
dans le
réelles ne
s'annulant pas sur M. La structure algébrique est préservée : le
produit tensoriel des fibrés en droites est la somme (plutôt multiplication)
dans le  , le fibré dual est l'opposé (l'inverse).
, le fibré dual est l'opposé (l'inverse).
Maintenant, on a envie de dire qu'une fonction à valeurs dans 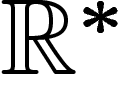 est, en cohomologie, la même chose qu'une fonction à valeurs dans
est, en cohomologie, la même chose qu'une fonction à valeurs dans
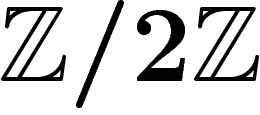 . Pour cela, il suffit de considérer le faisceau
. Pour cela, il suffit de considérer le faisceau  des
fonctions réelles sur M, et de constater que la suite de faisceaux
des
fonctions réelles sur M, et de constater que la suite de faisceaux
![\[
0 \ra \G \stackrel{\exp}{\ra} \F \ra \Z/2\Z \ra 0
\]](cech233.png)
 est un faisceau admettant des partitions
de l'unité, sa cohomologie en degré strictement positif est nulle ;
alors la suite exacte longue en cohomologie fournit un isomorphisme entre
est un faisceau admettant des partitions
de l'unité, sa cohomologie en degré strictement positif est nulle ;
alors la suite exacte longue en cohomologie fournit un isomorphisme entre
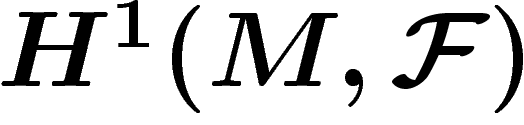 et
et 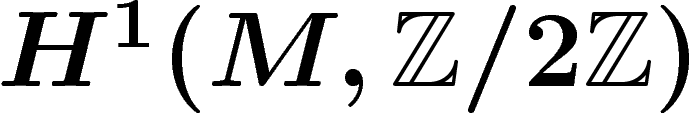 .
.
On a donc démontré que l'ensemble des fibrés en droites réelles sur une
variété M s'identifie à 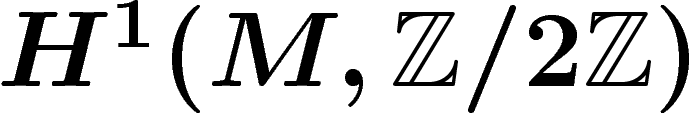 . On va s'attaquer aux fibrés
complexes. La situation sera plus compliquée, et ce sont en fait des
éléments du
. On va s'attaquer aux fibrés
complexes. La situation sera plus compliquée, et ce sont en fait des
éléments du  (les premières classes de Chern) qui vont naturellement
intervenir.
(les premières classes de Chern) qui vont naturellement
intervenir.
Variétés complexes. Les variétés complexes sont définies de
la même manière que les variétés réelles, en demandant que localement, on
ait une identification à des ouverts de  , et que les changements de
carte soient holomorphes. En chaque point on peut définir des
coordonnées locales
, et que les changements de
carte soient holomorphes. En chaque point on peut définir des
coordonnées locales 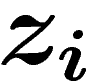 et
et 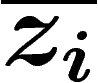 , et le fibré tangent
complexe est
, et le fibré tangent
complexe est ![$\ds \C\left[ \frac{\partial}{\partial z_i},
\frac{\partial}{\partial \overline{z_i}} \right]$](cech242.png) .
.
On notera T le fibré tangent (ou TM en cas d'ambiguïté), et 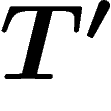 et
et
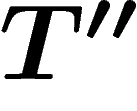 les parties holomorphe et antiholomorphe de ce fibré, localement
engendrées par les
les parties holomorphe et antiholomorphe de ce fibré, localement
engendrées par les 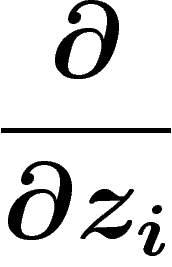 et les
et les
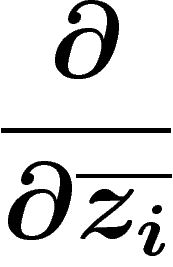 respectivement. La
décomposition
respectivement. La
décomposition 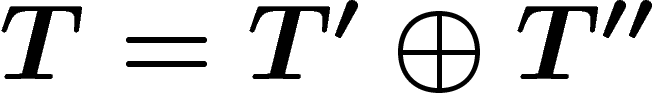 est stable par les applications
holomorphes entre variétés (c'est une condition nécessaire et suffisante
pour qu'une application entre variétés complexes soit holomorphe).
est stable par les applications
holomorphes entre variétés (c'est une condition nécessaire et suffisante
pour qu'une application entre variétés complexes soit holomorphe).
On notera également  le fibré cotangent et
sa décomposition en parties holomorphe et antiholomorphe.
le fibré cotangent et
sa décomposition en parties holomorphe et antiholomorphe.
Une forme différentielle de degré p est une section globale 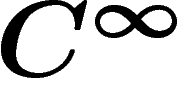 du fibré
du fibré 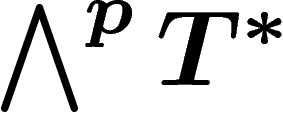 Les formes différentielles sont localement
des produits extérieurs de
Les formes différentielles sont localement
des produits extérieurs de 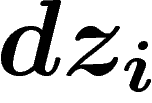 et
et 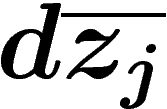 , multipliées par
des coefficients
, multipliées par
des coefficients 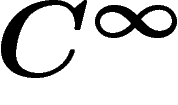 . On notera
. On notera 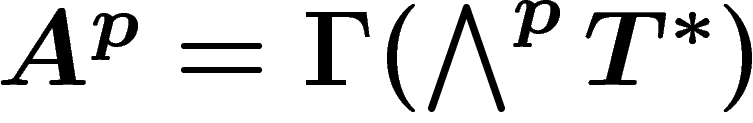 .
On notera aussi
.
On notera aussi 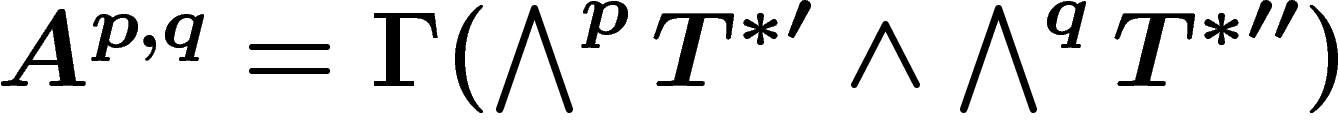 les formes s'écrivant localement comme produit extérieur de
p formes holomorphes et de q formes antiholomorphes de degré 1.
les formes s'écrivant localement comme produit extérieur de
p formes holomorphes et de q formes antiholomorphes de degré 1.
La différentielle extérieure est localement définie par 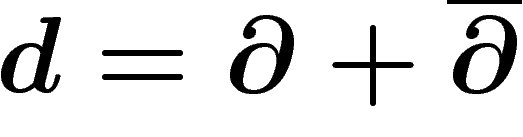 où (I et J sont des multi-indices) :
où (I et J sont des multi-indices) :
![\[
\d (\phi\, dz_I \wedge d\overline{z}_J)=\sum_i \frac{\d \phi}{\d z_i}\, dz_i
\wedge dz_I \wedge d\overline{z}_J
\]](cech257.png)
![\[
\overline{\d} (\phi\, dz_I \wedge d\overline{z}_J)=\sum_i \frac{\d \phi}{\d
\overline{z_i}}\, dz_i
\wedge dz_I \wedge d\overline{z}_J
\]](cech258.png)
 étant une fonction
étant une fonction 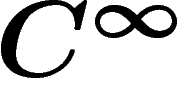 .
.
Fibrés hermitiens. Un fibré hermitien est un fibré complexe
dont chaque fibre est munie d'un produit scalaire hermitien. En d'autres
termes, si E est un fibré complexe de base M, une structure
hermitienne est un élément de 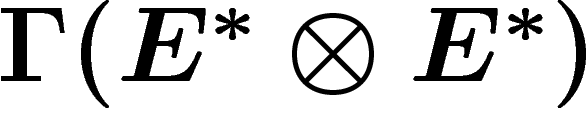 hermitien
dans chaque fibre, où
hermitien
dans chaque fibre, où 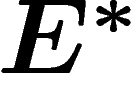 désigne le fibré dual de E.
désigne le fibré dual de E.
On notera 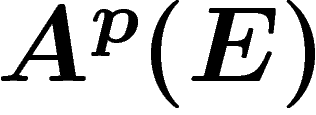 les p-formes différentielles sur la base M à
valeurs dans le fibré E, autrement dit, les sections du fibré
les p-formes différentielles sur la base M à
valeurs dans le fibré E, autrement dit, les sections du fibré
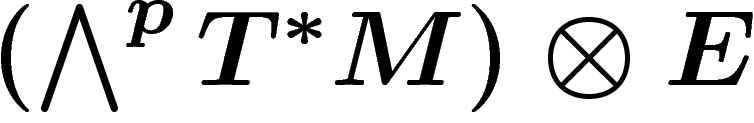 . Il convient toujours de ne
pas confondre
. Il convient toujours de ne
pas confondre 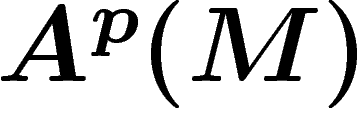 et
et 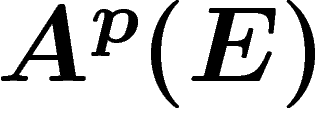 .
.
Il est à noter que sur un fibré
hermitien, l'opérateur 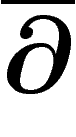 est canoniquement défini (mais par
est canoniquement défini (mais par
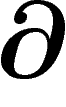 ) : pour cela, constatons que les éléments de
) : pour cela, constatons que les éléments de 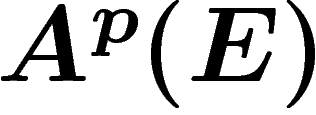 s'écrivent
localement comme combinaison linéaire d'éléments de la forme
s'écrivent
localement comme combinaison linéaire d'éléments de la forme
 où
où  est un élément de
est un élément de 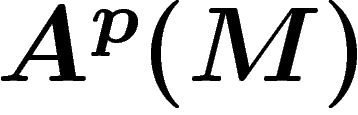 et e une
section holomorphe de E ; déclarons que l'opérateur
et e une
section holomorphe de E ; déclarons que l'opérateur
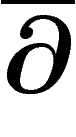 appliqué à une section holomorphe donne 0 et posons donc
appliqué à une section holomorphe donne 0 et posons donc
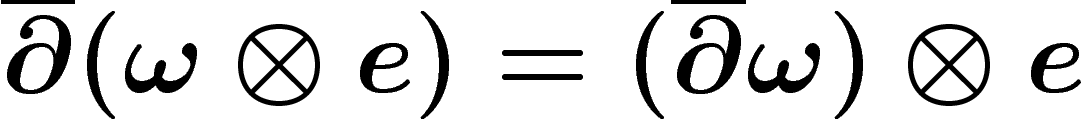 .
.
Connexions. Une connexion sur un fibré est une manière de comparer des fibres voisines (ce qu'on ne peut faire canoniquement), ou encore une manière de dériver des sections du fibré par rapport à un vecteur de la base : a priori, on voudrait pour dériver former la différence des valeurs de la section en des points de fibres infiniment voisines, mais cela ne peut pas se faire canoniquement.
Précisément, une connexion est une application 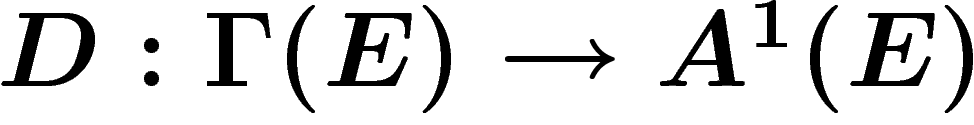 satisfaisant la règle de Leibnitz : pour toute fonction
satisfaisant la règle de Leibnitz : pour toute fonction  sur
M et pour toute section
sur
M et pour toute section 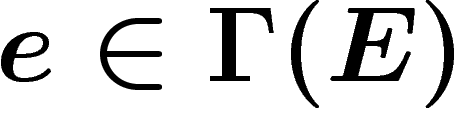 ,
,
![\[
D(f.e)=df\otimes e + f.De \ \ \in A^1(E)
\]](cech278.png)
Alors, si v est un vecteur tangent de la base au point 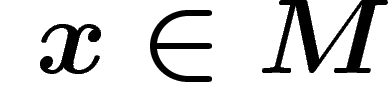 , la
dérivée de la section e dans la direction v est
, la
dérivée de la section e dans la direction v est 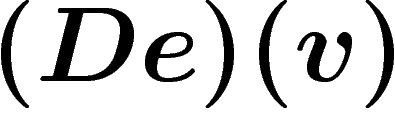 qui est un
élément de la fibre en x.
qui est un
élément de la fibre en x.
Une connexion définit aussi une notion de transport parallèle d'un vecteur de la fibre le long d'une courbe de la base : on dit que le vecteur est transporté parallèlement à lui-même si sa dérivée par rapport au vecteur tangent à la courbe est nulle.
Une fois donnée une connexion sur E, on peut étendre cette dérivation
aux p-formes à valeurs dans E en posant par définition la règle de
Leibnitz : pour 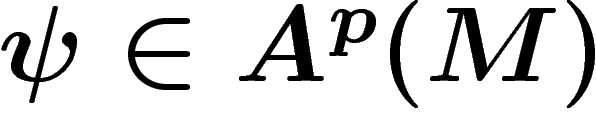 et
et 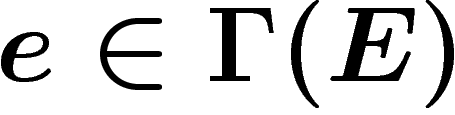 , on définit la
dérivée de
, on définit la
dérivée de  par
par
![\[
D(\psi \otimes e) = d\psi \otimes e + (-1)^p\, \psi \wedge De \ \ \in
A^{p+1}(E)
\]](cech284.png)
Courbure. Soit un fibré hermitien E de base M, muni d'une
connexion D. On notera  le produit hermitien sur les
fibres. On dit que la connexion est compatible avec la structure
hermitienne si pour toutes sections
le produit hermitien sur les
fibres. On dit que la connexion est compatible avec la structure
hermitienne si pour toutes sections 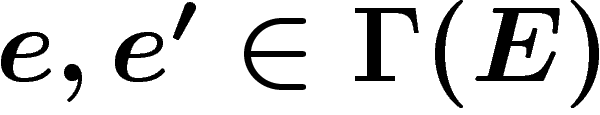 , on a
, on a
![\[
d\langle e,f \rangle=\langle De,f\rangle + \langle e,Df \rangle \ \ \in
A^1(M)
\]](cech287.png)
En utilisant la décomposition en parties holomorphe et antiholomorphe
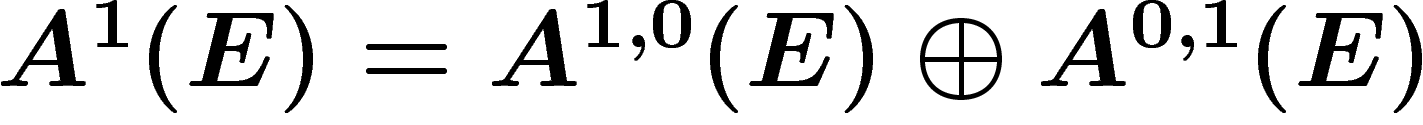 , on peut définir les parties
holomorphe
, on peut définir les parties
holomorphe  et antiholomorphe
et antiholomorphe  de D. On dit que D est
compatible avec la structure complexe si
de D. On dit que D est
compatible avec la structure complexe si 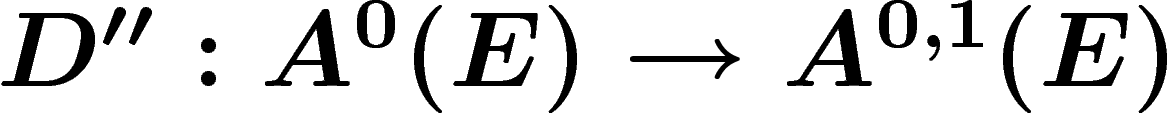 est
égal à l'opérateur
est
égal à l'opérateur 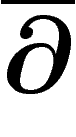 défini ci-dessus.
défini ci-dessus.
Un fibré hermitien peut être canoniquement muni d'une connexion. En effet, un lemme classique (cf. [GH]) affirme que sur un fibré hermitien, il existe une unique connexion compatible avec la structure complexe et avec la structure hermitienne. Ce sera toujours celle-là que nous considérerons par la suite.
Pour définir la courbure, on commence par regarder
la composée de la connexion 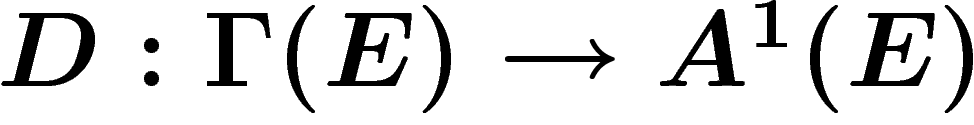 et
et 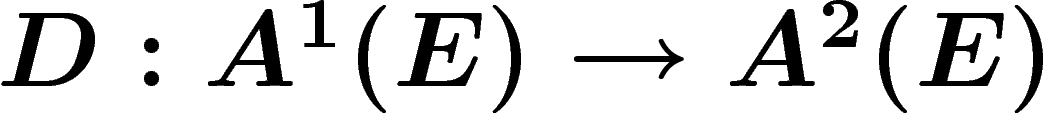 qui à toute section
qui à toute section 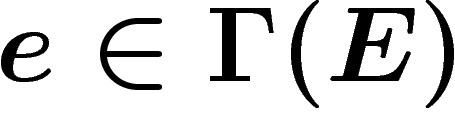 associe
associe 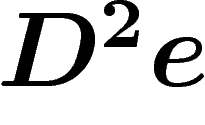 , qui est une
2-forme sur M à valeurs dans E.
, qui est une
2-forme sur M à valeurs dans E.
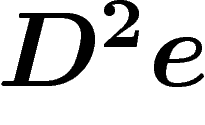 appliqué à un couple de vecteurs
appliqué à un couple de vecteurs 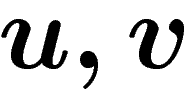 tangents à la base,
s'interprète (au signe près) comme la variation du vecteur e de la
fibre lorsqu'on le transporte parallèlement le long du vecteur u, puis
de v, puis de
tangents à la base,
s'interprète (au signe près) comme la variation du vecteur e de la
fibre lorsqu'on le transporte parallèlement le long du vecteur u, puis
de v, puis de 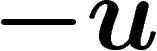 , puis de
, puis de 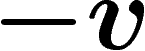 . Sur une surface courbée dans
l'espace, on voit que si on prend un vecteur (par exemple un vecteur
tangent) et qu'on le transporte parallèlement à lui-même suivant une
boucle de la surface (« parallèlement » dans la surface et non dans
l'espace ambiant), on ne va pas revenir sur le même vecteur. La courbure
décrit ce phénomène.
. Sur une surface courbée dans
l'espace, on voit que si on prend un vecteur (par exemple un vecteur
tangent) et qu'on le transporte parallèlement à lui-même suivant une
boucle de la surface (« parallèlement » dans la surface et non dans
l'espace ambiant), on ne va pas revenir sur le même vecteur. La courbure
décrit ce phénomène.
Par un petit miracle, en chaque point, la valeur de 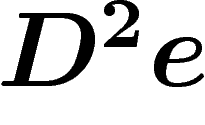 ne dépend que
de la valeur de la section e en ce point, et pas des valeurs voisines.
En effet,
ne dépend que
de la valeur de la section e en ce point, et pas des valeurs voisines.
En effet, 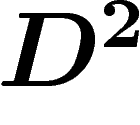 est
est 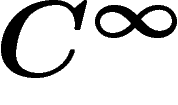 -linéaire : si
-linéaire : si 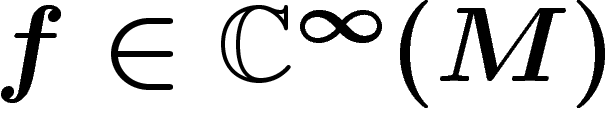 et
et 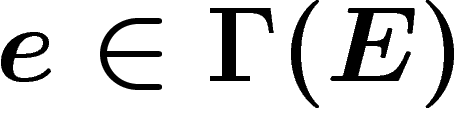 , on a
, on a
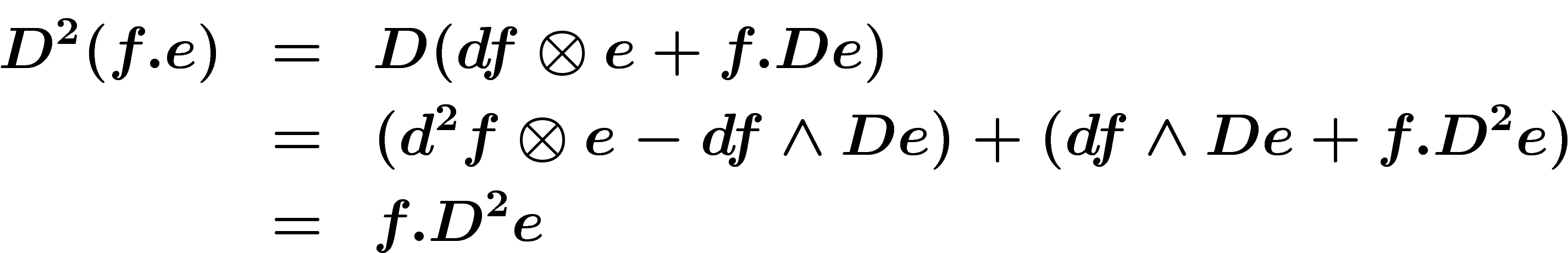
Par conséquent, si deux sections e et 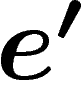 ont même valeur en un point,
ont même valeur en un point,
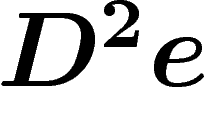 et
et 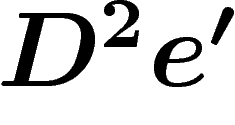 ont la même valeur. Autrement dit,
l'application
ont la même valeur. Autrement dit,
l'application  provient d'une
application du fibré E dans le fibré
provient d'une
application du fibré E dans le fibré 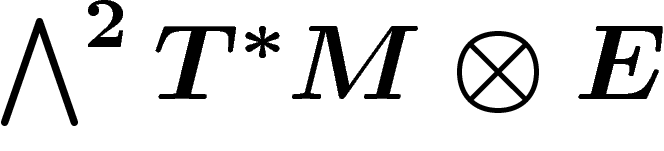 définie au-dessus de chaque point de la base. Formulé encore
autrement,
définie au-dessus de chaque point de la base. Formulé encore
autrement, 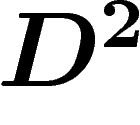 définit une section globale
définit une section globale  du fibré
du fibré
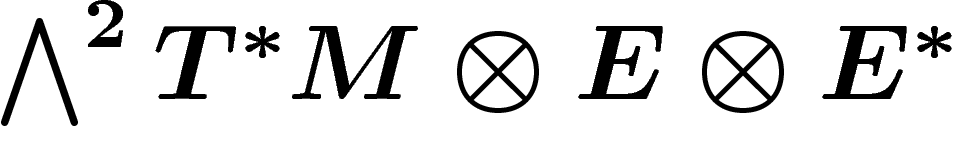 .
.
La forme  est appelée la forme de courbure du fibré. Elle associe
à tout couple de vecteurs tangents à la base au point x une application
linéaire de la fibre en x dans elle-même.
est appelée la forme de courbure du fibré. Elle associe
à tout couple de vecteurs tangents à la base au point x une application
linéaire de la fibre en x dans elle-même.
Si l'on travaille en coordonnées : on peut prendre des sections
 formant une base orthonormée au voisinage d'un point.
Alors la connection D définit des coefficients
formant une base orthonormée au voisinage d'un point.
Alors la connection D définit des coefficients 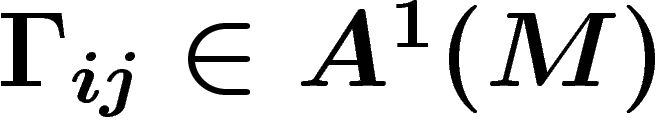 par
par
![\[
De_i=\sum \Gamma_{ij}\otimes e_j \ \ \in A^1(E)
\]](cech318.png)
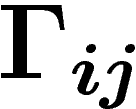 dépendent de l'ensemble des sections orthonormées
choisies et non seulement de leur valeur en un point.
dépendent de l'ensemble des sections orthonormées
choisies et non seulement de leur valeur en un point.
Un calcul direct montre alors que
![\[\Theta e_i=\sum_j
\left(d\Gamma_{ij}-\sum_k\Gamma_{ik}\wedge\Gamma_{kj}\right) \otimes e_j
\ \ \in A^2(E)
\]](cech320.png)
 dans cette base s'écrit comme la différentielle de la matrice
(de 1-formes)
dans cette base s'écrit comme la différentielle de la matrice
(de 1-formes) 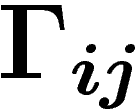 , moins le produit extérieur (formel) de cette
matrice avec elle-même.
, moins le produit extérieur (formel) de cette
matrice avec elle-même.
Soit M une variété complexe. On désignera par  le faisceau des fonctions
holomorphes et par
le faisceau des fonctions
holomorphes et par 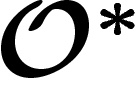 celui (multiplicatif) des fonctions
holomorphes ne s'annulant pas sur M. On rappelle qu'on exige d'un fibré
complexe que ses changements de carte soient holomorphes.
celui (multiplicatif) des fonctions
holomorphes ne s'annulant pas sur M. On rappelle qu'on exige d'un fibré
complexe que ses changements de carte soient holomorphes.
Exactement pour la même raison que pour les fibrés en droites réels,
l'ensemble des fibrés en droites complexes sur M s'identifie à
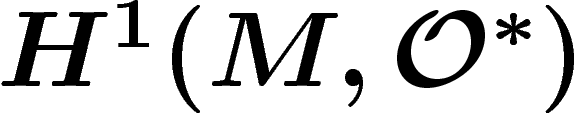 . Cette identification respecte les fibrés duals et le
produit tensoriel.
. Cette identification respecte les fibrés duals et le
produit tensoriel.
On a une suite exacte de faisceaux
![\[
0 \ra \Z \ra \O \stackrel{\exp}{\ra} \O^\ast \ra 0
\]](cech326.png)
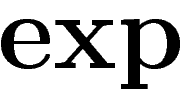 représente
représente 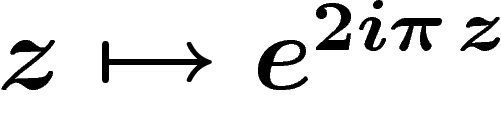 .
.
Cette suite exacte de faisceaux donne en cohomologie un opérateur bord
![\[
\d : H^1(M,\O^\ast) \ra H^2(M,\Z)
\]](cech329.png)
Si 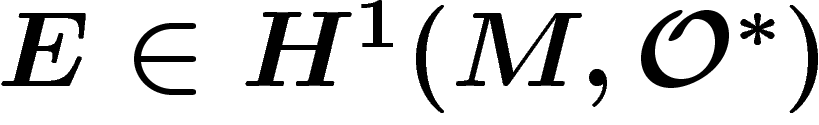 est un fibré, sa première classe de Chern est
définie comme
est un fibré, sa première classe de Chern est
définie comme 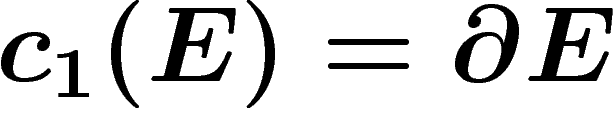 .
.
Prenons un exemple. Plaçons-nous sur la sphère de Riemann
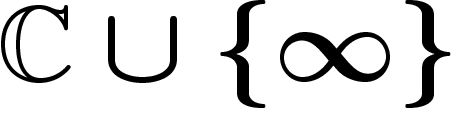 et considérons un recouvrement à deux ouverts, l'un
étant le disque de rayon 1 dans
et considérons un recouvrement à deux ouverts, l'un
étant le disque de rayon 1 dans  un peu élargi, l'autre son
complémentaire un peu élargi. L'intersection est un anneau. Prenons deux
trivialisations, et prenons z comme fonction de transition entre ces
trivialisations. On voit bien ce qui se passe : en recollant les deux
trivialisations, on fait faire un tour au fibré quand on tourne autour de
l'origine. La classe de Chern de ce fibré est 1 dans
un peu élargi, l'autre son
complémentaire un peu élargi. L'intersection est un anneau. Prenons deux
trivialisations, et prenons z comme fonction de transition entre ces
trivialisations. On voit bien ce qui se passe : en recollant les deux
trivialisations, on fait faire un tour au fibré quand on tourne autour de
l'origine. La classe de Chern de ce fibré est 1 dans
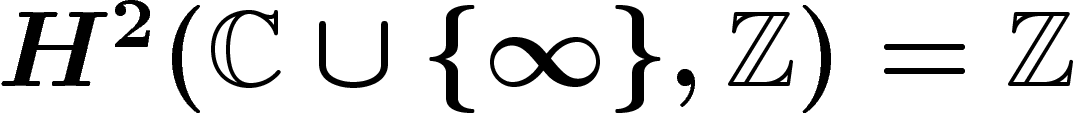 . La classe de Chern compte combien de tours
le fibré fait autour de chaque 2-cavité de M.
. La classe de Chern compte combien de tours
le fibré fait autour de chaque 2-cavité de M.
On a évidemment 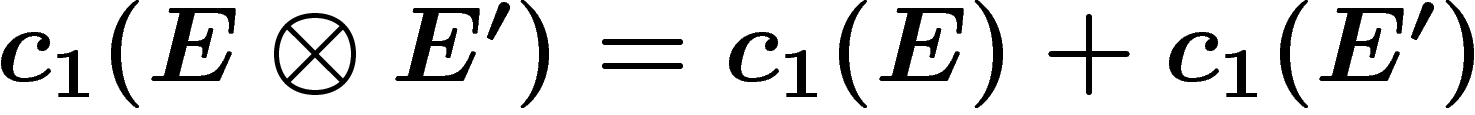 et
et
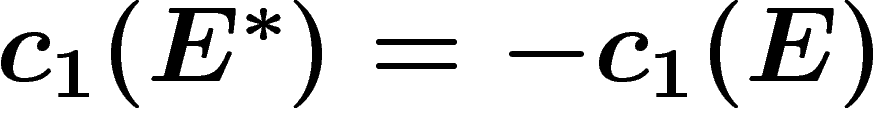 .
.
En outre, on peut montrer qu'un fibré en droites complexes est déterminé,
à isomorphisme 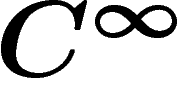 (mais non holomorphe), par sa classe de Chern.
(mais non holomorphe), par sa classe de Chern.
Soit E un fibré en droites sur une variété M, muni d'une connexion
quelconque. Soit  sa courbure.
sa courbure.  est une section du fibré
est une section du fibré 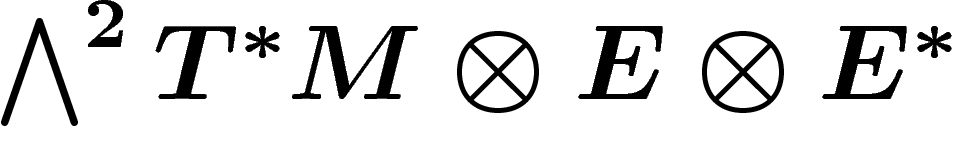 , or comme le fibré est de dimension 1,
, or comme le fibré est de dimension 1,
 est (canoniquement !) isomorphe à
est (canoniquement !) isomorphe à 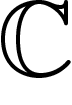 .
.
 est donc simplement une 2-forme différentielle sur M.
est donc simplement une 2-forme différentielle sur M.
On a vu que localement,  s'écrivait sous la forme
s'écrivait sous la forme
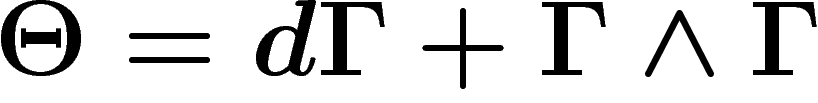 où
où 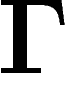 est une (matrice
est une (matrice  dont l'entrée est une) 1-forme. On a
dont l'entrée est une) 1-forme. On a 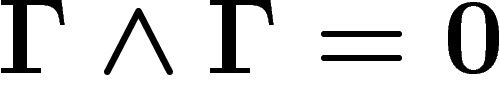 et donc
et donc
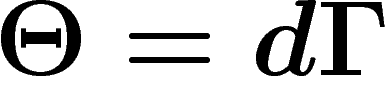 , autrement dit,
, autrement dit,  est localement exacte, donc
fermée.
est localement exacte, donc
fermée.
La forme de courbure d'un fibré en droites complexes est ainsi une
2-forme fermée sur la base. On peut donc considérer sa classe en
cohomologie de De Rham ![$[\Theta] \in H^2_{DR}(M)$](cech351.png) .
.
Par ailleurs, la classe de Chern du fibré, 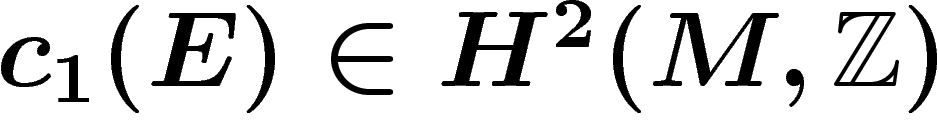 , peut
être vue comme un élément de
, peut
être vue comme un élément de 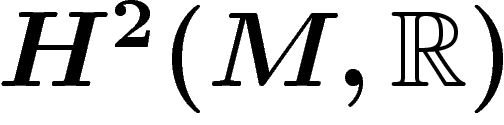 , qui s'identifie à
, qui s'identifie à 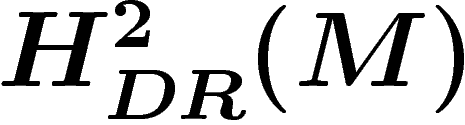 d'après le théorème de De Rham démontré ci-dessus.
d'après le théorème de De Rham démontré ci-dessus.
Théorème -- Ces deux classes de cohomologie peuvent être comparées :
![\[
c_1(E)=\frac{i}{2\pi}\, \Theta \ \ \in H^2_{DR}(M)
\]](cech355.png)
Ce théorème est évidemment à rapprocher de celui de Gauss-Bonnet.
Démonstration. Calculons d'abord la classe de Chern. Soit
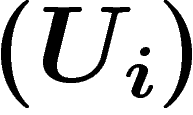 un recouvrement ouvert de M donnant une trivialisation de E,
assez fin pour que les intersections
un recouvrement ouvert de M donnant une trivialisation de E,
assez fin pour que les intersections  soient simplement
connexes. Soient
soient simplement
connexes. Soient 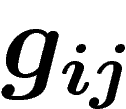 les fonctions de transition entre ouverts.
les fonctions de transition entre ouverts.
Maintenant, reprenons la définition de la classe de Chern en cohomologie :
![\[
c_1=\d : H^1(M,\O^\ast) \ra H^2(M,\Z)
\]](cech359.png)
![\[
0 \ra \Z \ra \O \stackrel{\exp}{\ra} \O^\ast \ra 0
\]](cech360.png)
Le bord du cocycle 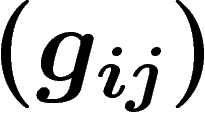 est nul, on
veut prendre, par logarithme, son bord dans
est nul, on
veut prendre, par logarithme, son bord dans 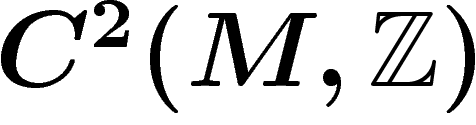 , qui provient
des différentes déterminations du logarithme. C'est le cocycle
, qui provient
des différentes déterminations du logarithme. C'est le cocycle
![\[
z_{ijk}=\frac{1}{2i\pi}(\log g_{jk}-\log g_{ik} +
\log g_{ij})
\]](cech363.png)
Travaillons maintenant sur la connexion. Prenons sur l'ouvert 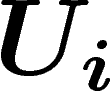 la
section donnée par
la
section donnée par 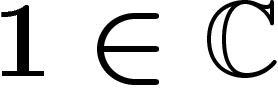 dans la trivialisation, que nous notons
dans la trivialisation, que nous notons
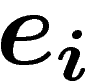 . Sur
. Sur  , on a par définifiont
, on a par définifiont 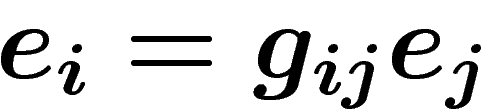 .
.
La connexion est localement donnée par une 1-forme 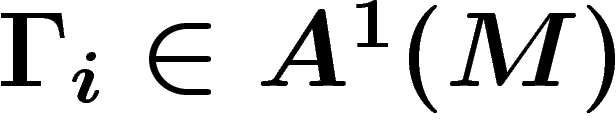 telle que
telle que
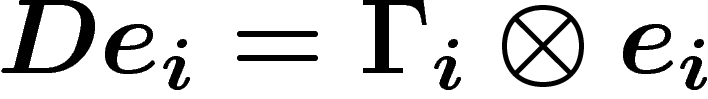 (nous sommes en dimension 1...). Sur
(nous sommes en dimension 1...). Sur  , on a
, on a
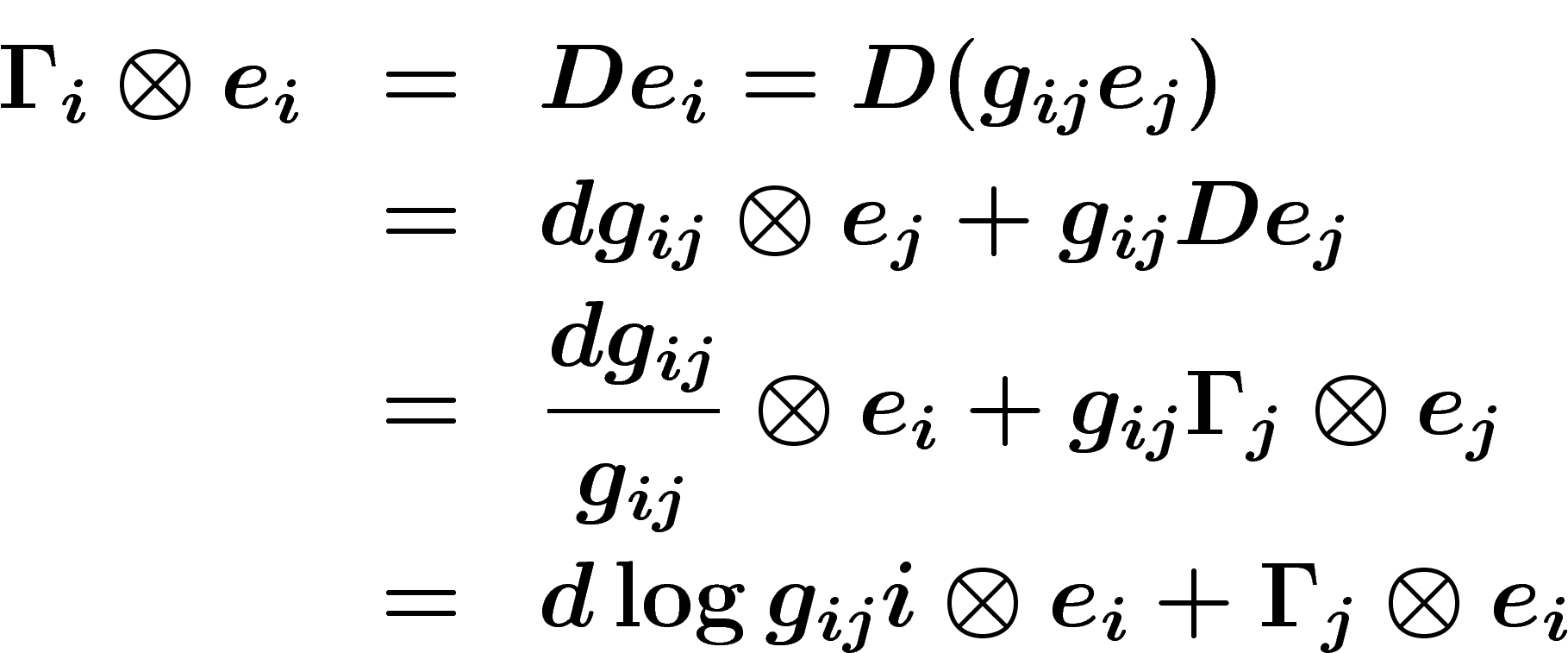
On a donc la loi de transformation des 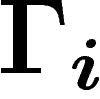 , ou encore le bord de
la 0-chaîne
, ou encore le bord de
la 0-chaîne 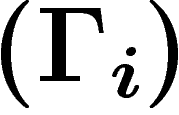 :
:
![\[
\Gamma_i-\Gamma_j=d \log g_{ij}
\]](cech375.png)
La forme de courbure est alors 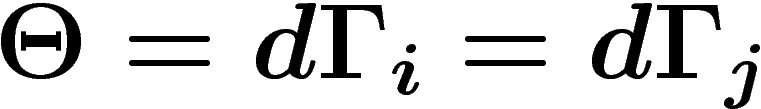 , globalement
définie.
, globalement
définie.
On a ainsi des formes plus ou moins explicites, d'une part, pour la
classe de Chern, donnée par le 2-cocycle
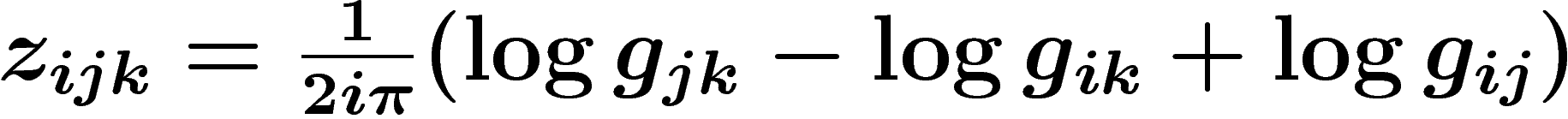 , et d'autre part pour la courbure
, et d'autre part pour la courbure  donnée comme une
2-forme différentielle
donnée comme une
2-forme différentielle 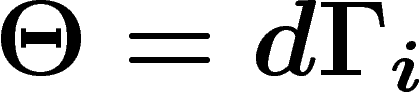 avec
avec 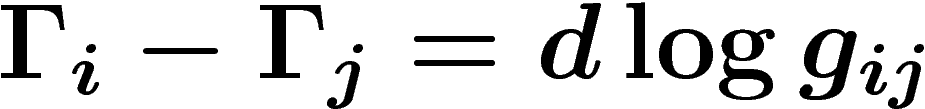 . Pour obtenir l'égalité, il faut désormais expliciter
l'isomorphisme de De Rham démontré plus haut. Nous allons donc partir de
la 2-forme
. Pour obtenir l'égalité, il faut désormais expliciter
l'isomorphisme de De Rham démontré plus haut. Nous allons donc partir de
la 2-forme  .
.
Une première partie de l'isomorphisme provenait de la suite exacte
![\[
0
\ra \Zz^1 \hookrightarrow \Omega^1 \stackrel{d}{\ra} \Zz^2 \ra 0
\]](cech382.png)
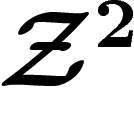 ,
autrement dit une 2-forme fermée (par exemple
,
autrement dit une 2-forme fermée (par exemple  ...), un élément de
...), un élément de
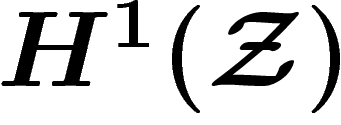 :
:
![\[
H^0(\Zz^2) \stackrel{\d}{\ra} H^1(\Zz^1)
\]](cech386.png)
 localement, sur chaque ouvert, comme la différentielle d'une
1-forme ; prendre le bord de cette 0-chaîne de 1-formes, c'est
l'opérateur bord cherché. Notre écriture locale de
localement, sur chaque ouvert, comme la différentielle d'une
1-forme ; prendre le bord de cette 0-chaîne de 1-formes, c'est
l'opérateur bord cherché. Notre écriture locale de  comme
différentielle est toute trouvée : on a
comme
différentielle est toute trouvée : on a 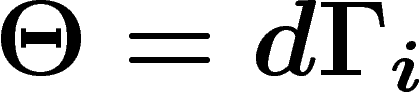 sur
sur 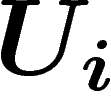 . Le
bord de cette 0-chaîne de 1-formes est bien sûr la 1-chaîne
. Le
bord de cette 0-chaîne de 1-formes est bien sûr la 1-chaîne
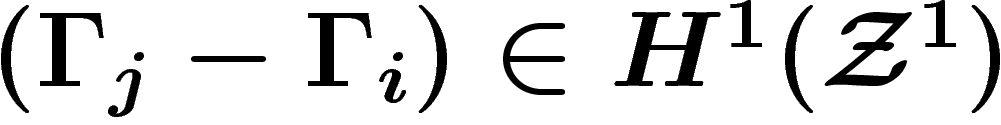 , autrement dit
, autrement dit 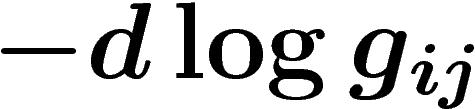 .
.
L'autre partie de l'isomorphisme provenait de la suite exacte
![\[
0 \ra \R \hookrightarrow \Omega^0 \stackrel{d}{\ra} \Zz^1 \ra 0
\]](cech393.png)
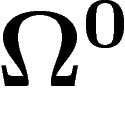 est le faisceau des
est le faisceau des  -formes, autrement dit des fonctions
-formes, autrement dit des fonctions
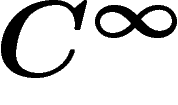 ), qui fournit elle aussi un opérateur bord
), qui fournit elle aussi un opérateur bord 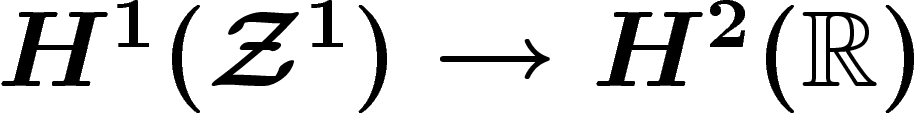 , obtenu en écrivant une 1-chaîne de 1-formes, localement, comme
une 1-chaîne de différentielles de fonctions, et en prenant le bord de
cette 1-chaîne. Là encore, notre 1-chaîne
, obtenu en écrivant une 1-chaîne de 1-formes, localement, comme
une 1-chaîne de différentielles de fonctions, et en prenant le bord de
cette 1-chaîne. Là encore, notre 1-chaîne 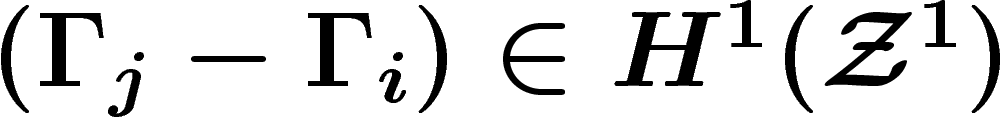 est toute écrite comme différentielle locale de fonctions
puisque
est toute écrite comme différentielle locale de fonctions
puisque 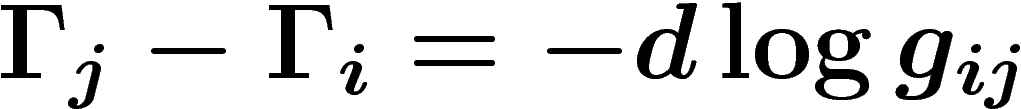 . On doit donc prendre le bord
de la 1-chaîne de fonctions
. On doit donc prendre le bord
de la 1-chaîne de fonctions 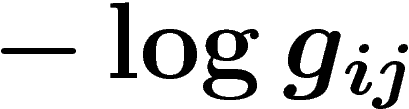 , ce qui donne, bien entendu,
, ce qui donne, bien entendu,
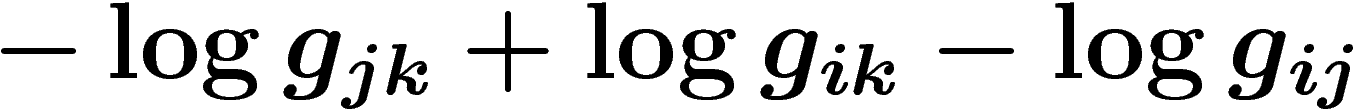 , ce qui démontre le théorème.
, ce qui démontre le théorème.
[G]R. Godement, Topologie algébrique et théorie des faisceaux, Hermann, Paris (1958).
[GH]P. Griffiths, J. Harris, Principles of algebraic geometry, Wiley, New York (1978).