 de [Gro1].
de [Gro1].
Yann Ollivier, octobre 2000
Aussi au format pdf ou postscript gzippé
Le leitmotiv est le suivant : sur certains espaces de grande dimension,
une fonction lipschitzienne est presque constante. « Presque » signifie
que l'espace concerné est doté d'une mesure canonique et que sur une
partie de mesure très grande, la fonction considérée est très proche
d'une certaine valeur. Toutes ces idées sont décrites dans le chapitre
 de [Gro1].
de [Gro1].
L'exemple le plus connu d'une telle situation est la loi des grands
nombres : on prend un grand nombre n de variables aléatoires
identiquement distribuées à valeur dans un espace X (qui reçoit donc
une mesure), et on considère des fonctions « naturelles » (la moyenne, le
sup...) sur l'espace 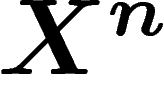 des résultats de n tirages : ces fonctions
sont, avec une probabilité proche de 1, très proches d'une certaine
valeur (l'espérance de la variable, par exemple). Voir à ce propos
l'excellent article de M. Talagrand, A new look at independence
([Tal]), qui donne un théorème de concentration des fonctions
lipschitziennes sur tout espace de probabilité de la forme
des résultats de n tirages : ces fonctions
sont, avec une probabilité proche de 1, très proches d'une certaine
valeur (l'espérance de la variable, par exemple). Voir à ce propos
l'excellent article de M. Talagrand, A new look at independence
([Tal]), qui donne un théorème de concentration des fonctions
lipschitziennes sur tout espace de probabilité de la forme 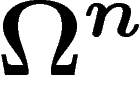 .
.
Un autre exemple (similaire) est celui de la physique statistique : sur l'espace des états d'un gaz, par exemple, toutes les fonctions physiquement intéressantes (pression, température, entropie...) sont bien définies, bien qu'il existe des configurations possibles, extrêmement improbables, qui donneraient des valeurs fort différentes mais jamais observées.
M. Gromov a placé ces idées dans un contexte géométrique. Étant donné un espace métrique mesuré, il définit la notion de « diamètre observable » : c'est l'amplitude maximale de variation d'une fonction 1-lipschitzienne définie sur cet espace, si l'on s'autorise à ne pas tenir compte d'une partie de l'espace de faible mesure où cette fonction aurait des valeurs exceptionnelles.
Plus précisément, si X est un espace métrique mesuré, de mesure 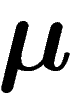 normalisée à 1, si l'on se fixe un paramètre
normalisée à 1, si l'on se fixe un paramètre 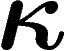 représentant la proportion de mesure qu'on s'autorise à négliger :
représentant la proportion de mesure qu'on s'autorise à négliger :
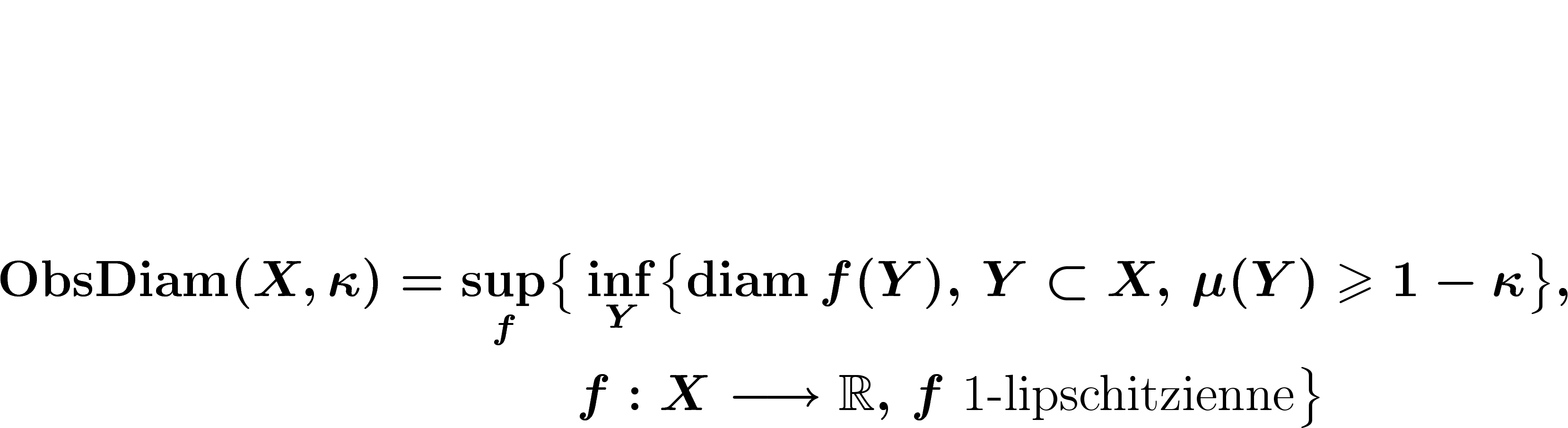
Si on avait la mauvaise foi de prendre 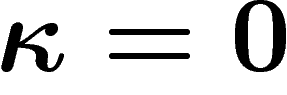 , on trouverait
évidemment le diamètre ordinaire de l'espace X (plus exactement le
diamètre essentiel de X où on retire une partie de mesure nulle). Ce
qui nous intéresse est bien sûr de prendre
, on trouverait
évidemment le diamètre ordinaire de l'espace X (plus exactement le
diamètre essentiel de X où on retire une partie de mesure nulle). Ce
qui nous intéresse est bien sûr de prendre 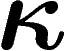 petit mais non nul.
petit mais non nul.
On remarque alors souvent que le diamètre observable est nettement plus
petit que le diamètre habituel. Par exemple, pour la sphère de dimension
n et de rayon 1, le diamètre observable est de l'ordre de 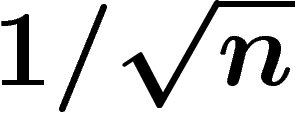 .
La dépendance en
.
La dépendance en 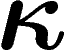 ressemble souvent à un facteur
ressemble souvent à un facteur
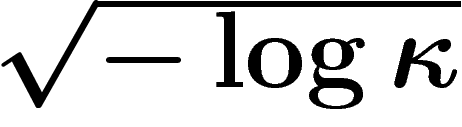 (cas où la masse des points à une distance
supérieure à d décroît comme
(cas où la masse des points à une distance
supérieure à d décroît comme 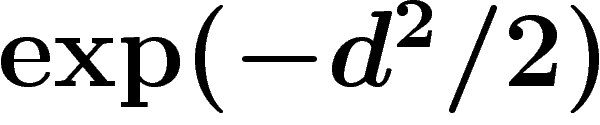 ), ce qui croît lentement
quand
), ce qui croît lentement
quand 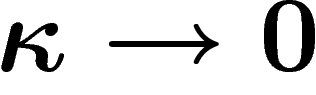 ; aussi omettra-t-on souvent de mentionner
; aussi omettra-t-on souvent de mentionner
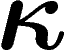 .
.
Considérons la sphère 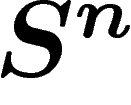 , n grand, de rayon 1, avec la mesure
canonique normalisée à 1. Un calcul rapide montre que presque toute la
masse de la sphère est située à une distance inférieure à
, n grand, de rayon 1, avec la mesure
canonique normalisée à 1. Un calcul rapide montre que presque toute la
masse de la sphère est située à une distance inférieure à 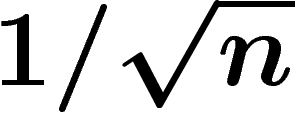 du
plan médian.
du
plan médian.
Plus exactement, la loi de la distance d'un point au plan
médian est très proche d'une gaussienne d'écart-type 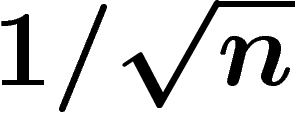 . Cette
constatation est ancienne (cf. [Lev]).
. Cette
constatation est ancienne (cf. [Lev]).
Pour transformer cela en évaluation du diamètre observable, il est
nécessaire de faire intervenir le théorème isopérimétrique sur la sphère :
parmi les parties de 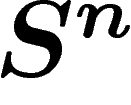 de volume donné, celles dont le volume du bord
(ou de manière équivalente, le volume d'un
de volume donné, celles dont le volume du bord
(ou de manière équivalente, le volume d'un  -voisinage) est le plus
petit sont les calottes (jolie démonstration dans [FLM]).
-voisinage) est le plus
petit sont les calottes (jolie démonstration dans [FLM]).
En particulier, si on a une partie de mesure 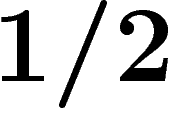 , on est sûr qu'un
, on est sûr qu'un
 -voisinage de cette partie contiendra au moins autant de volume
qu'un
-voisinage de cette partie contiendra au moins autant de volume
qu'un  -voisinage d'une demi-sphère ; or on a vu que pour
-voisinage d'une demi-sphère ; or on a vu que pour 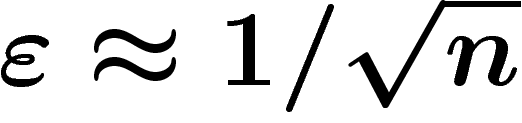 , un
, un  -voisinage de l'équateur (donc a fortiori
d'une demi-sphère) contenait presque toute la mesure.
-voisinage de l'équateur (donc a fortiori
d'une demi-sphère) contenait presque toute la mesure.
L'évaluation du diamètre observable va alors comme suit : prenons une
fonction f sur 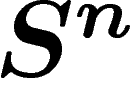 1-lipschitzienne. Soit
1-lipschitzienne. Soit 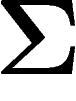 l'ensemble des
points où f est inférieure à sa médiane. Par définition de la médiane,
l'ensemble des
points où f est inférieure à sa médiane. Par définition de la médiane,
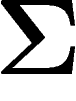 est de volume
est de volume 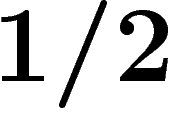 (quitte à retirer des points où f est
précisément égale à sa médiane).
(quitte à retirer des points où f est
précisément égale à sa médiane).
Fixons le paramètre  pour le diamètre observable, et prenons
pour le diamètre observable, et prenons
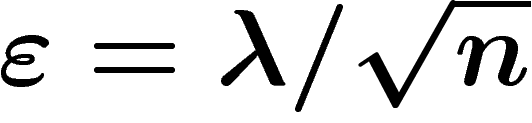 tel qu'un
tel qu'un  -voisinage d'une partie de volume
-voisinage d'une partie de volume
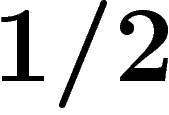 de la sphère contienne presque tout le volume de la sphère, à
de la sphère contienne presque tout le volume de la sphère, à
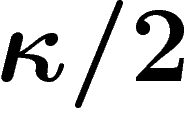 près.
près.
Alors, sauf sur un ensemble de mesure inférieure à 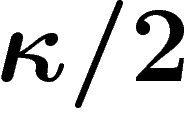 , tout point
de la sphère est distant de moins de
, tout point
de la sphère est distant de moins de  d'un point de
d'un point de 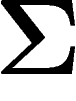 . Sur
. Sur
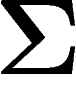 , f est inférieure à sa médiane, et comme f est
1-lipschitzienne, cela implique que f est inférieure à sa médiane plus
, f est inférieure à sa médiane, et comme f est
1-lipschitzienne, cela implique que f est inférieure à sa médiane plus
 , sauf sur un ensemble de mesure inférieure à
, sauf sur un ensemble de mesure inférieure à 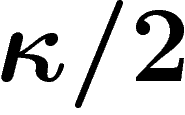 . En
recommençant dans l'autre sens, si m est la médiane de f, on a prouvé
qu'en-dehors d'un ensemble de mesure inférieure à
. En
recommençant dans l'autre sens, si m est la médiane de f, on a prouvé
qu'en-dehors d'un ensemble de mesure inférieure à 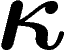 , f est
comprise entre
, f est
comprise entre 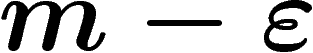 et
et 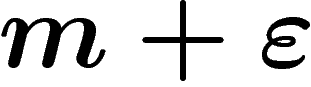 .
.
En utilisant la formule gaussienne résultant du calcul que nous n'avons pas fait pour la concentration sur la sphère, on trouve ainsi que :
![\[
\ObsDiam (S^n,\kappa)\leq \frac{2\sqrt{2}}{\sqrt{n-1}}
\sqrt{-\log(\kappa/4)}
\]](introdea043.png)
De plus, en considérant la fonction « projection sur un axe de
coordonnées », on voit que cette évaluation en 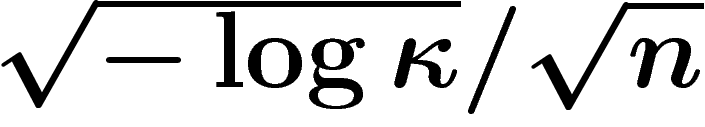 est correcte à un facteur constant près.
est correcte à un facteur constant près.
Tout ceci se transpose en fait au cas d'une variété riemannienne à
courbure strictement positive (cf. [Gro2]). Soit V une
variété de dimension n de courbure de Ricci partout supérieure à
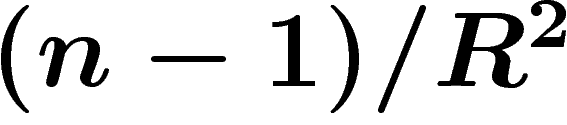 (courbure de Ricci d'une sphère de rayon R). Alors
(courbure de Ricci d'une sphère de rayon R). Alors
![\[
\ObsDiam (V,\kappa)\leq R\, \frac{2\sqrt{2}}{\sqrt{n-1}}
\sqrt{-\log(\kappa/4)}
\]](introdea046.png)
Jusqu'ici, rien que de très élémentaire. On va désormais s'attacher à
évaluer le diamètre observable de sous-variétés de  .
.
On a deux choix de métrique pour une sous-variété X de 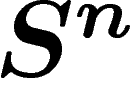 : soit
restreindre directement la fonction distance héritée de
: soit
restreindre directement la fonction distance héritée de 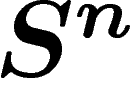 , soit
prendre la métrique intrinsèque de X, qui est celle de
, soit
prendre la métrique intrinsèque de X, qui est celle de
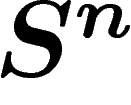 où l'on ne s'autorise qu'à suivre des chemins à l'intérieur X.
où l'on ne s'autorise qu'à suivre des chemins à l'intérieur X.
Dans un premier temps, on ne s'intéressera qu'à la première, où la
distance entre deux points de X est simplement leur distance dans
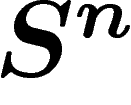 . Ce cas est beaucoup plus simple à traiter ; une évaluation du
diamètre pour la métrique intrinsèque est connue uniquement dans le cas
de sous-variétés algébriques de
. Ce cas est beaucoup plus simple à traiter ; une évaluation du
diamètre pour la métrique intrinsèque est connue uniquement dans le cas
de sous-variétés algébriques de 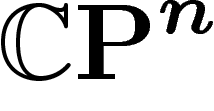 , l'algébricité offrant
plus de prise.
, l'algébricité offrant
plus de prise.
Soit donc X une sous-variété de 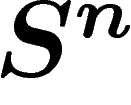 , de dimension
, de dimension 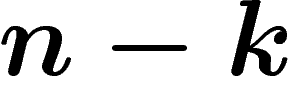 . On
s'intéresse à la codimension k, autrement dit à des sous-variétés
données par k équations, point de vue plus adapté au cadre algébrique
adopté ensuite. On supposera que cette codimension est assez petite.
Sinon, si par exemple X est un cercle (de dimension 1, codimension
. On
s'intéresse à la codimension k, autrement dit à des sous-variétés
données par k équations, point de vue plus adapté au cadre algébrique
adopté ensuite. On supposera que cette codimension est assez petite.
Sinon, si par exemple X est un cercle (de dimension 1, codimension
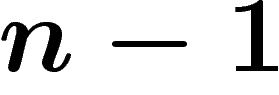 ), son diamètre observable est de l'ordre de
), son diamètre observable est de l'ordre de 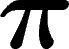 (petite
dimension, pas de concentration...).
(petite
dimension, pas de concentration...).
On fait en outre les hypothèses suivantes :
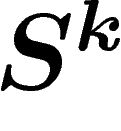 est une sphère équatoriale de
est une sphère équatoriale de 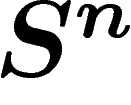 (sous-sphère de même
rayon), de dimension k complémentaire de X, alors
(sous-sphère de même
rayon), de dimension k complémentaire de X, alors 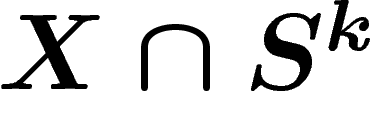 contient au plus d points (si l'intersection est transverse) ;
contient au plus d points (si l'intersection est transverse) ;
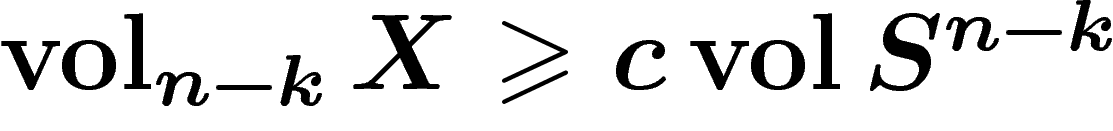 .
.
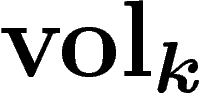 désigne la mesure de volume usuelle en dimension k.
désigne la mesure de volume usuelle en dimension k.
La première condition est l'analogue d'une condition de degré dans le cas algébrique.
La seconde condition tient au fait que si l'on prend des parties très
petites de 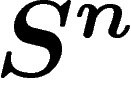 , la géométrie globale de
, la géométrie globale de 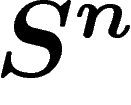 qui force la petitesse du
diamètre observable ne joue plus, et que le diamètre observable peut très
bien être de l'ordre de
qui force la petitesse du
diamètre observable ne joue plus, et que le diamètre observable peut très
bien être de l'ordre de 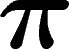 comme le diamètre ordinaire.
comme le diamètre ordinaire.
Le principe du raisonnement (que nous n'exposerons pas en entier) est que
pour tout espace X, le diamètre observable 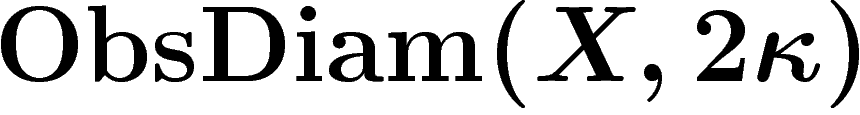 est
inférieur à la distance maximale entre deux parties de X de mesure
(relative) supérieure à
est
inférieur à la distance maximale entre deux parties de X de mesure
(relative) supérieure à 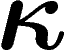 (cela résulte très simplement de la
définition : si on a une fonction 1-lipschitzienne, on prend les
ensembles de mesure
(cela résulte très simplement de la
définition : si on a une fonction 1-lipschitzienne, on prend les
ensembles de mesure 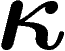 où cette fonction est la plus grande et la
plus petite ; si leur distance est inférieure à D, le diamètre
observable est inférieur à D).
où cette fonction est la plus grande et la
plus petite ; si leur distance est inférieure à D, le diamètre
observable est inférieur à D).
On prend donc deux parties de X de mesure 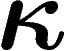 (par rapport à
la mesure sur la sous-variété X). On utilise ce qu'on
sait déjà sur
(par rapport à
la mesure sur la sous-variété X). On utilise ce qu'on
sait déjà sur 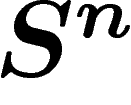 pour évaluer la distance entre ces deux parties. Pour
cela, on prend un
pour évaluer la distance entre ces deux parties. Pour
cela, on prend un  -voisinage de ces parties dans
-voisinage de ces parties dans 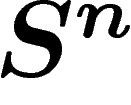 . On évalue
le volume de ces deux voisinages : grâce au faible diamètre observable de
. On évalue
le volume de ces deux voisinages : grâce au faible diamètre observable de
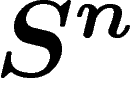 , on sait que même si ce volume n'est pas très grand, ces deux
parties devront être proches l'une de l'autre. Il ne reste alors plus
qu'à constater que la distance entre les deux parties de départ est
inférieure à
, on sait que même si ce volume n'est pas très grand, ces deux
parties devront être proches l'une de l'autre. Il ne reste alors plus
qu'à constater que la distance entre les deux parties de départ est
inférieure à 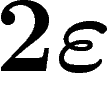 plus la distance entre leurs
plus la distance entre leurs  -voisinages ;
d'où l'on déduira que le diamètre observable de X est faible.
-voisinages ;
d'où l'on déduira que le diamètre observable de X est faible.
![\begin{center}
\includegraphics[scale=0.25]{XinSn.eps}
\end{center}](introdea076.png)
Les paramètres c et d des hypothèses interviennent dans l'évaluation
du volume du  -voisinage des parties considérées.
Donnons seulement le résultat final :
-voisinage des parties considérées.
Donnons seulement le résultat final :
![\[
\ObsDiam(X,2\kappa)\leq \frac{4\sqrt{k}}{\sqrt{n}}\sqrt{\log
\left(\frac nk \left(\frac d{c\kappa}\right)^{2/k}\right)}
\]](introdea078.png)
Observons la dépendance en 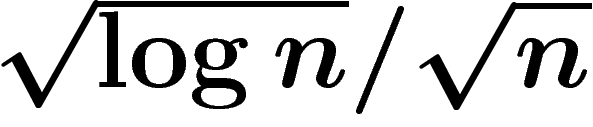 à
à 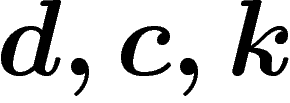 fixés (il
se pourrait que le
fixés (il
se pourrait que le 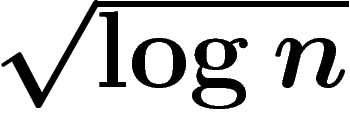 soit de trop).
soit de trop).
J'ai cherché pendant un certain temps à améliorer ce résultat, aussi bien qu'à essayer de trouver des exemples où cette évaluation serait correcte, sans succès. On rencontre des problèmes comme la taille maximale d'un voisinage tubulaire d'une sous-variété, ou le nombre de calottes disjointes de rayon donné qu'on peut disposer sur une sphère.
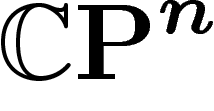
On va désormais considérer le cas de l'espace projectif complexe 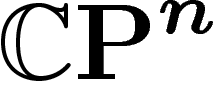 ,
avec sa métrique et sa mesure canoniques.
,
avec sa métrique et sa mesure canoniques.
D'abord, il est immédiat d'après la définition du diamètre observable,
que si 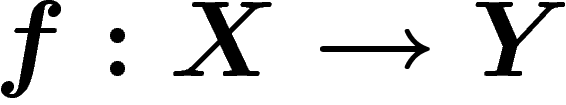 est une application 1-lipschitzienne entre
deux espaces métriques mesurés qui envoie la mesure de X sur la mesure
de Y, alors le diamètre observable de Y est inférieur à celui de X.
En utilisant l'application standard
est une application 1-lipschitzienne entre
deux espaces métriques mesurés qui envoie la mesure de X sur la mesure
de Y, alors le diamètre observable de Y est inférieur à celui de X.
En utilisant l'application standard 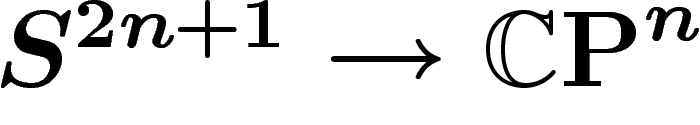 , qui
envoie bien la mesure canonique de
, qui
envoie bien la mesure canonique de 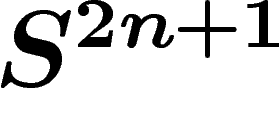 sur celle de
sur celle de 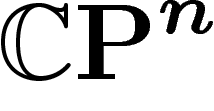 , on
obtient donc que le diamètre observable de
, on
obtient donc que le diamètre observable de 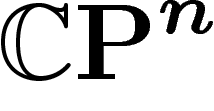 est inférieur à celui
de
est inférieur à celui
de 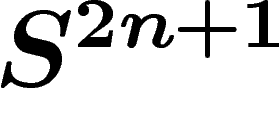 .
.
Ensuite, pour ce qui est des sous-variétés algébriques avec la métrique
directement restreinte de 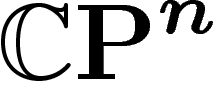 , notre travail sur la sphère se
transpose directement (avec des constantes légèrement différentes dans le
résultat final, qui se trouve en outre simplifié par le fait que pour une
variété algébrique, le volume c par rapport à celui du projectif est
exactement égal au degré d --- théorème de Wirtinger, voir par
exemple [GH]), l'hypothèse sur le nombre d'intersections avec
une sous-sphère devenant ici exactement une borne sur le degré de notre
sous-variété algébrique.
, notre travail sur la sphère se
transpose directement (avec des constantes légèrement différentes dans le
résultat final, qui se trouve en outre simplifié par le fait que pour une
variété algébrique, le volume c par rapport à celui du projectif est
exactement égal au degré d --- théorème de Wirtinger, voir par
exemple [GH]), l'hypothèse sur le nombre d'intersections avec
une sous-sphère devenant ici exactement une borne sur le degré de notre
sous-variété algébrique.
On s'intéresse donc désormais aux sous-variétés algébriques de 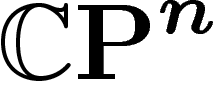 avec leur métrique propre, c'est-à-dire la métrique où la distance entre
deux points est la longueur du plus petit arc inclus dans la
sous-variété joignant ces points.
avec leur métrique propre, c'est-à-dire la métrique où la distance entre
deux points est la longueur du plus petit arc inclus dans la
sous-variété joignant ces points.
Il se trouve que l'algébricité permet, par une méthode assez complexe, d'estimer le diamètre observable pour cette métrique. La méthode comporte six (6) étapes que nous allons succinctement exposer.
Soit donc 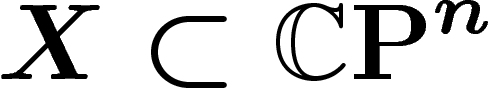 une sous-variété algébrique complexe de
codimension k et de degré d. Soit encore
une sous-variété algébrique complexe de
codimension k et de degré d. Soit encore 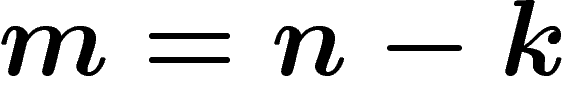 la dimension
(complexe) de X. L'idée est de comparer X avec un sous-espace
projectif
la dimension
(complexe) de X. L'idée est de comparer X avec un sous-espace
projectif 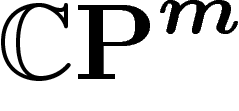 : on va projeter X orthogonalement sur un
: on va projeter X orthogonalement sur un 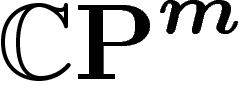 en
position bien choisie, et on va essayer de contrôler le sort que fait
subir cette projection à la métrique de X (a priori, cette projection
peut beaucoup augmenter les distances, comme le fait la projection
orthogonale de points proches d'un pôle sur l'équateur d'une sphère).
Voici les étapes annoncées :
en
position bien choisie, et on va essayer de contrôler le sort que fait
subir cette projection à la métrique de X (a priori, cette projection
peut beaucoup augmenter les distances, comme le fait la projection
orthogonale de points proches d'un pôle sur l'équateur d'une sphère).
Voici les étapes annoncées :
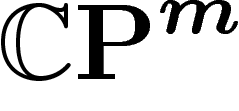 est le quotient projectif d'un espace linéaire
est le quotient projectif d'un espace linéaire  . Le « centre » de la projection orthogonale sur
. Le « centre » de la projection orthogonale sur 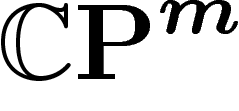 est
l'orthogonal de ce
est
l'orthogonal de ce 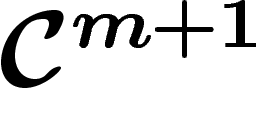 ; ils se déterminent mutuellement. On tient
évidemment à ce que notre sous-variété X soit assez éloignée de ce
centre, sinon la projection par ce centre fera exploser les distances. Il
s'agit donc de trouver un sous-espace
; ils se déterminent mutuellement. On tient
évidemment à ce que notre sous-variété X soit assez éloignée de ce
centre, sinon la projection par ce centre fera exploser les distances. Il
s'agit donc de trouver un sous-espace 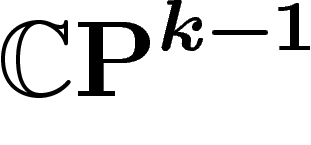 de dimension
complémentaire de X, aussi distant de X que possible. On montre par
récurrence qu'il en existe un à distance
de dimension
complémentaire de X, aussi distant de X que possible. On montre par
récurrence qu'il en existe un à distance 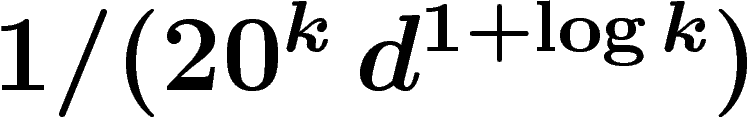 , ce qui
n'est probablement pas optimal mais mieux que rien. Nous avons donc
choisi notre
, ce qui
n'est probablement pas optimal mais mieux que rien. Nous avons donc
choisi notre 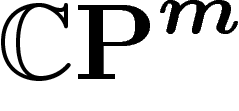 .
.
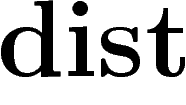 la distance usuelle sur
la distance usuelle sur 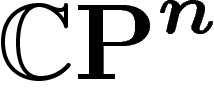 . On montre alors
que la projection orthogonale de deux points de X sur notre
. On montre alors
que la projection orthogonale de deux points de X sur notre 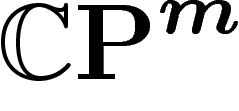 dilate la
distance X d'un facteur au plus
dilate la
distance X d'un facteur au plus 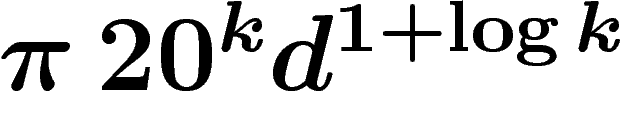 .
.
 (comme « projetée »), définie comme la distance usuelle
entre les projetés de deux points sur
(comme « projetée »), définie comme la distance usuelle
entre les projetés de deux points sur 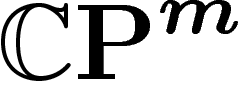 , et l'autre,
, et l'autre, 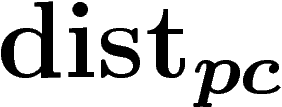 ou
« projetée, par chemins » comme la longueur pour
ou
« projetée, par chemins » comme la longueur pour  du plus court
arc inclus dans X joignant deux points. Par construction on a
du plus court
arc inclus dans X joignant deux points. Par construction on a
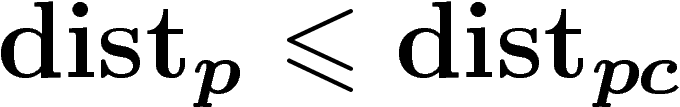 . Maintenant, on cherche à contrôler
. Maintenant, on cherche à contrôler 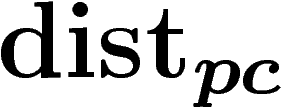 par
par  . Pour cela, on va se restreindre à une partie
. Pour cela, on va se restreindre à une partie 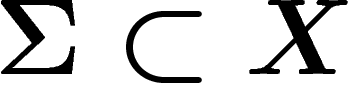 , définie comme l'ensemble des antécédents des points de
, définie comme l'ensemble des antécédents des points de
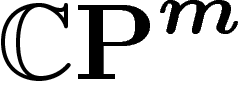 n'ayant qu'un antécédent dans X par la projection
(génériquement, un point de
n'ayant qu'un antécédent dans X par la projection
(génériquement, un point de 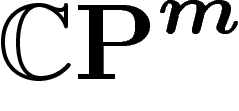 a d antécédents par cette
projection). Alors, dès que
a d antécédents par cette
projection). Alors, dès que 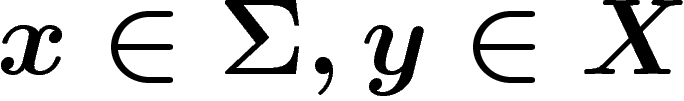 , on a
, on a
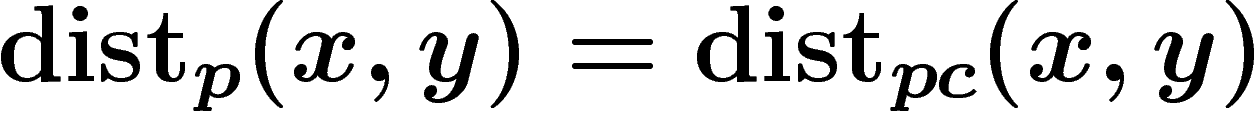 .
.
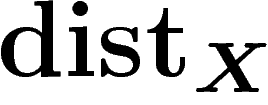 sur X.
On veut la contrôler par
sur X.
On veut la contrôler par 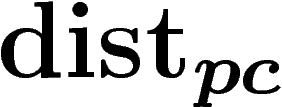 . On montre que
. On montre que 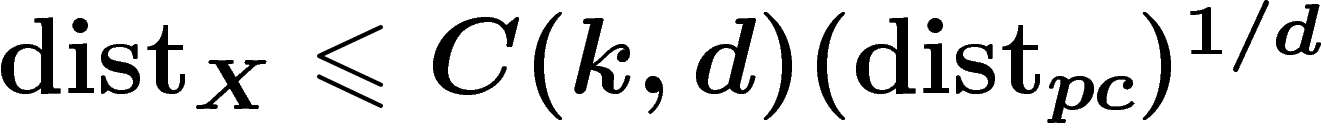 . La puissance
. La puissance 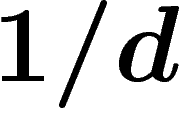 provient du fait qu'aux points où
X est parallèle à la direction de projection, la projection s'assimile
à une puissance d-ième. Cette étape est particulièrement intriquée et
fait intervenir divers résultats de géométrie complexe sur les positions
de racines de polynômes.
provient du fait qu'aux points où
X est parallèle à la direction de projection, la projection s'assimile
à une puissance d-ième. Cette étape est particulièrement intriquée et
fait intervenir divers résultats de géométrie complexe sur les positions
de racines de polynômes.
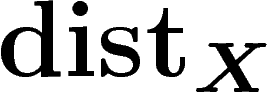 par
par
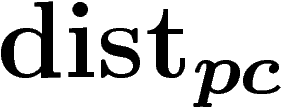 , de
, de 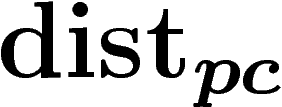 par
par  (sur une sous-partie
(sur une sous-partie 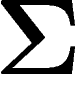 seulement), et de
seulement), et de  par la distance habituelle
par la distance habituelle 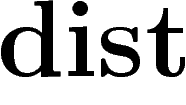 , on a
réussi enfin (sur
, on a
réussi enfin (sur 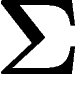 ) à contrôler la métrique intrinsèque de X
par la métrique de
) à contrôler la métrique intrinsèque de X
par la métrique de 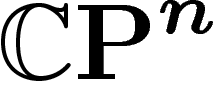 . Maintenant, il faut prouver que
. Maintenant, il faut prouver que 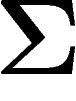 est
assez gros pour ce que l'on veut en faire, au sens où beaucoup de points
de X sont
est
assez gros pour ce que l'on veut en faire, au sens où beaucoup de points
de X sont  -proches de
-proches de 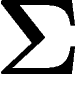 ; ce qui se fait avec des
techniques semblables à celles employées pour les sous-variétés de
; ce qui se fait avec des
techniques semblables à celles employées pour les sous-variétés de 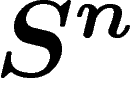 .
.
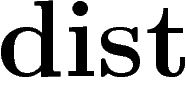 , la majoration de
, la majoration de 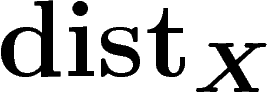 par
par 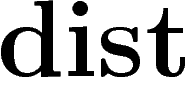 sur
sur
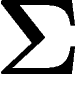 et le fait que beaucoup de points de X sont proches de
et le fait que beaucoup de points de X sont proches de
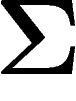 pour en déduire une majoration du diamètre observable de X
pour la métrique
pour en déduire une majoration du diamètre observable de X
pour la métrique 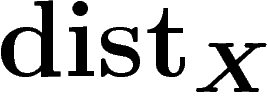 .
.
On a ainsi démontré, pour 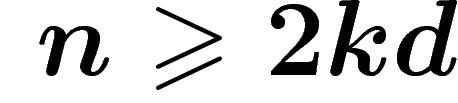 (condition issue de la
démonstration) :
(condition issue de la
démonstration) :
![\[
\ObsDiam(X,\kappa)_{\dist_X}\leq C(k,d) \left(-\frac kn \log
\left(\kappa^{1/k}\frac kn\right)\right)^{1/2d}
\]](introdea143.png)
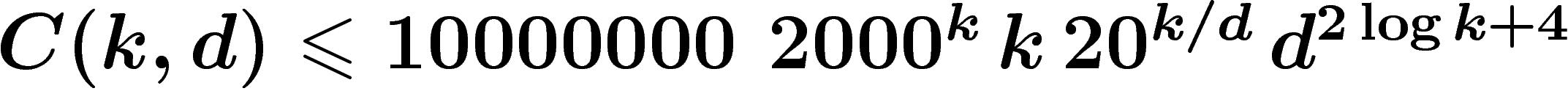 .
.
On voit qu'à k et d fixés,
![\[\ObsDiam(X)_{\dist_X}\lesssim
\left(\frac{\log n}{n}\right)^{1/2d}\]](introdea145.png)
Rappelons que
![\[\ObsDiam(X)_{\dist}
\lesssim \sqrt{\frac{\log n}{n}}\]](introdea146.png)
On ne sait pas du tout dans quelle mesure ce résultat est précis.
[FLM] T. Figiel, J. Lindenstrauss, V. Milman, The dimension of almost spherical sections of convex bodies, Acta Math. 139 (1977), p. 53--94.
[GH] P. Griffiths, J. Harris, Principles of algebraic geometry, Wiley, New York (1978).
[Gro1] M. Gromov, Metric structures for Riemannian and non-Riemannian spaces, Progress in Math. 152, Birkhäuser, Boston (1999).
[Gro2] M. Gromov, Isoperimetric inequalities in Riemannian manifolds, in Asymtotic theory of finite dimensional normed spaces, V. Milman et G. Schechtman, Lecture Notes in Mathematics 1200, Springer-Verlag, Berlin (1986).
[Lév] P. Lévy, Leçons d'analyse fonctionnelle, Gauthier-Villars, Paris (1922), réédité en 1951 sous le titre Problèmes concrets d'analyse fonctionnelle.
[Tal] M. Talagrand, A new look at independence, Ann. Prob. 24 (1996), 1, p. 1--37.