 ...).
...).
Ce texte est une présentation rapide et informelle des différentes notions de cohomologies qui seront exposées lors du groupe de travail, ainsi que de leurs motivations originelles et de quelques applications.
Aussi disponible au format pdf ou ps gzippé.
C'est dans un article de 1895 que Poincaré définit pour la première fois, sur les variétés différentielles, des chaînes (ou sous-variétés) qu'il qualifie d'homologues. Sa définition était assez imprécise, mais la notion qu'il utilisait recouvrait exactement l'acceptation actuelle : deux chaînes fermées sont homologues si leur différence est un bord.
Cependant, le texte de Poincaré ne faisait pas apparaître de cohomologie. La raison en est que sur une variété, on peut, par dualité de Poincaré, ramener complètement la cohomologie à l'homologie.
Les travaux de Poincaré ne restèrent pas inaperçus, mais ne furent pas
repris jusque dans les années 20. Durant la vingtaine d'années qui
suivirent, différentes théories (co)homologiques plus ou moins générales
et plus ou moins concurrentes
émergèrent (simpliciale, singulière,  ...).
...).
Le passage de l'homologie à la cohomologie était au départ une tentative de généralisation de la dualité de Poincaré. De manière très surprenante, les structures multiplicatives présentes sur les variétés différentiables se transposent très bien dans des situations plus abstraites en cohomologie (ce que l'homologie ne permet pas du tout).
Les années 40 virent l'apparition de l'algèbre homologique. Celle-ci contribua largement à l'apparition des notions de catégorie et de foncteur, omniprésentes en algèbre et en logique par la suite. L'invention de la cohomologie des faisceaux par Leray a eu le même succès dans toute la géométrie algébrique.
Diverses généralisations ont été imaginées : cohomologie des groupes (avec des connexions surprenantes avec la géométrie), cohomologie bornée, cohomologie équivariante, cohomologie étale... ce qui montre si besoin était que les notions cohomologiques se sont largement répandues dans presque toutes les mathématiques, et parfois jusqu'à la physique théorique.
Par la suite, on supposera connues l'homologie et la cohomologie singulières, auxquelles on se référera en l'absence de précision sur la théorie homologique utilisée (exposés d'introduction de Joël Riou).
Dualité de Poincaré (exposé de Charles-Antoine Louët). Sur une variété différentiable orientée,
on peut établir une correspondance très visuelle entre homologie et
cohomologie. En effet, si a et b sont deux chaînes de dimensions
complémentaires, on peut définir leur nombre d'intersection
 , comme le nombre de points d'intersection de a et b.
, comme le nombre de points d'intersection de a et b.
Cette définition n'a de sens que si a
et b sont lisses et placés en position générique (les points d'intersection sont
alors isolés et non dégénérés) ; mais on peut démontrer que ces
conditions peuvent être réalisées à l'intérieur de toute classe
d'homologie. Si en outre, on compte chaque point d'intersection avec un
signe 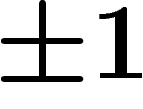 , en utilisant l'orientation de la variété, le nombre
, en utilisant l'orientation de la variété, le nombre
 ne dépend que des classes d'homologie de a et b.
ne dépend que des classes d'homologie de a et b.
Par dualité, on peut ainsi obtenir une cochaîne connaissant une chaîne :
la cochaîne 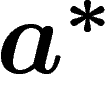 associée à a étant naturellement définie par
associée à a étant naturellement définie par
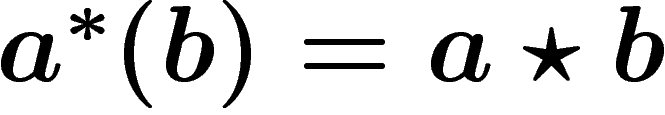 .
.
Ceci définit une correspondance entre homologie et cohomologie. On peut
aller plus loin : si la somme des dimensions de a et b est supérieure
à la dimension n de la variété ambiante, l'intersection  sera, en
position générique, une sous-variété de dimension
sera, en
position générique, une sous-variété de dimension 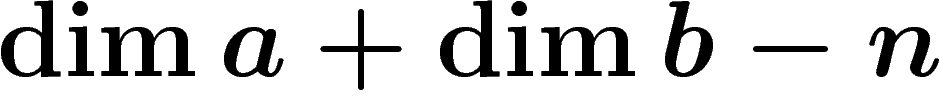 . En
comptant cette sous-variété avec les bons signes, on obtient une chaîne
en homologie, qui ne dépend que des classes d'homologie de a et b. En
passant aux duals
. En
comptant cette sous-variété avec les bons signes, on obtient une chaîne
en homologie, qui ne dépend que des classes d'homologie de a et b. En
passant aux duals 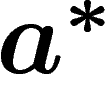 et
et 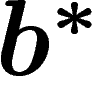 , et en notant
, et en notant  ,
,
 , on a ainsi défini une application bilinéaire de
, on a ainsi défini une application bilinéaire de  vers
vers 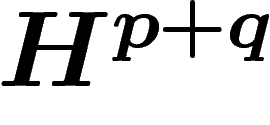 . C'est la structure multiplicative de la cohomologie.
. C'est la structure multiplicative de la cohomologie.
Structures multiplicatives (exposés de Joël Riou et Denis Conduché). Il est possible de généraliser ceci à une cohomologie quelconque, pas forcément sur une variété. Les résultats ne sont cependant pas aussi simples que ce que l'approche « naïve » peut laisser espérer : on a presque des isomorphismes, mais avec des termes supplémentaires.
Dans tout ce paragraphe, A sera un anneau principal et 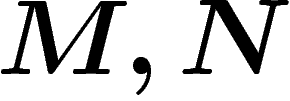 des
A-modules. Tout le problème vient du fait qu'en général, on n'obtient
pas une suite exacte si on tensorise une suite exacte par un même module,
ou si on prend les morphismes vers un même module.
Il est nécessaire d'ajouter des termes. Pour tout couple de modules M
et N, on peut définir des modules
des
A-modules. Tout le problème vient du fait qu'en général, on n'obtient
pas une suite exacte si on tensorise une suite exacte par un même module,
ou si on prend les morphismes vers un même module.
Il est nécessaire d'ajouter des termes. Pour tout couple de modules M
et N, on peut définir des modules 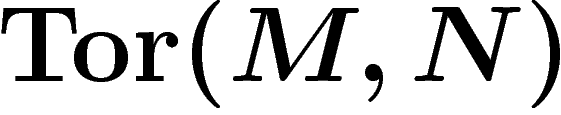 et
et 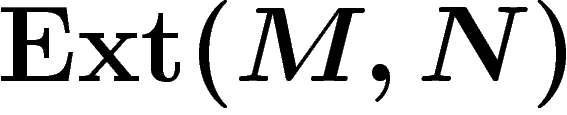 et un
opérateur
et un
opérateur 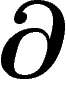 ayant la
propriété suivante : si
ayant la
propriété suivante : si
![\[
0 \ra M \ra M' \ra M''\ra 0
\]](cohom019.png)
![\[\begin{array}{ccccccccc}
0 &\ra& \Tor(M,N)&\ra&\Tor(M',N)&\ra&\Tor(M'',N)&\\ &\stackrel{\d}{\ra}&M\otimes
N&\ra& M'\otimes N&\ra& M''\otimes N&\ra& 0
\end{array}\]](cohom020.png)
![\[\begin{array}{ccccccccc}
0 &\la& \Ext(M,N) &\la& \Ext(M',N) &\la& \Ext(M'',N)
&\stackrel{\d}{\la}&\\
& & \Hom(M,N) &\la& \Hom(M',N) &\la& \Hom(M'',N) &\la& 0
\end{array}\]](cohom021.png)
Si les modules en question sont libres, ces contributions supplémentaires
se réduisent à  .
.
Ceci ouvre la voie à toutes les tensorisations dont on rêvait, par exemple pour calculer la cohomologie à valeurs dans M connaissant celle à valeurs dans A : on a une suite exacte
![\[
0\ra H_n(X,A) \otimes M \ra H_n(X,M) \ra \Tor(H_{n-1}(X,A),M) \ra 0
\]](cohom023.png)
![\[
0\la \Hom(H^n(X,A),M) \la H^n(X,M) \la \Ext(H_{n-1}(X,A),M) \la 0
\]](cohom024.png)
L'étape suivante pour obtenir de belles structures multiplicatives sur la cohomologie est d'arriver à envoyer le produit des cohomologies de deux espaces dans la cohomologie de l'espace produit. Pour la cohomologie singulière, cela se fait en prenant le produit des simplexes (qui n'en est pas un) et en décomposant le résultat en simplexes... Ne seraient les problèmes de torsion, on obtiendrait un isomorphisme, mais on écope d'une suite exacte (théorème de Künneth), qui plus est valable uniquement si l'un des deux espaces a une cohomologie de rang fini :
![\[
0 \ra \bigoplus_{p+q=n} H^p(X)\otimes H^q(Y) \ra H^n(X\times Y)
\stackrel{\d}{\ra} \bigoplus_{p+q=n+1} \Tor(H^p(X), H^q(Y)) \ra 0
\]](cohom025.png)
En particulier, en prenant 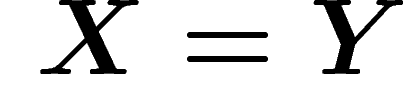 et en composant par l'application
diagonale
et en composant par l'application
diagonale 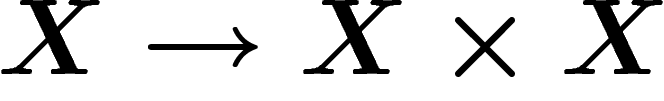 , on obtient une structure d'anneau sur la
cohomologie :
, on obtient une structure d'anneau sur la
cohomologie :
![\[
H^p(X)\otimes H^q(X) \ra H^{p+q}(X)
\]](cohom028.png)
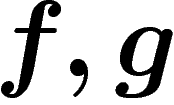 de degrés
de degrés 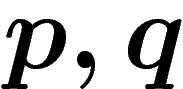 et une chaîne
et une chaîne  de degré
de degré  ,
à faire agir f sur le début de
,
à faire agir f sur le début de  et g sur la fin de
et g sur la fin de  .
.
Cohomologie de De Rham (exposé de Sandra Rozensztajn). Diverses constructions cohomologiques ont été proposées. L'une des plus importantes est la cohomologie de De Rham sur les variétés différentiables.
On considère l'espace tangent d'une variété (l'espace des vecteurs
infiniment petits en un point). On appelle d-forme une forme
d-linéaire antisymétrique sur cet espace (par exemple, dx est une
1-forme sur 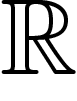 ).
).
On définit la différentielle 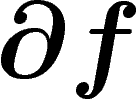 d'une d-forme f comme une
d'une d-forme f comme une  -forme
dont la valeur sur des vecteurs
-forme
dont la valeur sur des vecteurs  est obtenue comme suit :
on construit sur
est obtenue comme suit :
on construit sur  un
un  -parallélogramme
infinitésimal dans la variété ; chacune de ses faces est supportée par
d vecteurs, et donc, on peut calculer f sur ces faces ; on forme la
somme de f sur toutes les faces (avec des signes alternés ; c'est
plutôt une différence), et on divise par le volume infinitésimal du
parallélogramme. La valeur obtenue est
-parallélogramme
infinitésimal dans la variété ; chacune de ses faces est supportée par
d vecteurs, et donc, on peut calculer f sur ces faces ; on forme la
somme de f sur toutes les faces (avec des signes alternés ; c'est
plutôt une différence), et on divise par le volume infinitésimal du
parallélogramme. La valeur obtenue est 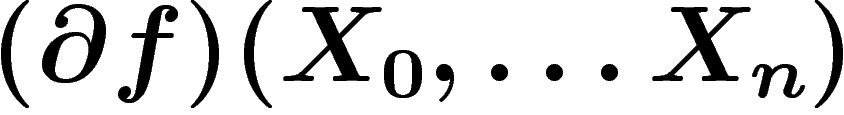 , sorte
de dérivée de f.
, sorte
de dérivée de f.
Si f est une d-forme, on peut l'intégrer sur une partie (lisse) de
dimension d de notre variété. Avec ces définitions, on a, en
particulier, la formule de Stokes : si X est une partie de la variété
qui est le bord d'une partie Y, l'intégrale sur X de f est égale à
l'intégrale de 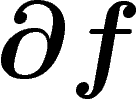 sur le bord de Y. (C'est une généralisation des formules de Green, d'Ostrogradski...)
sur le bord de Y. (C'est une généralisation des formules de Green, d'Ostrogradski...)
Maintenant, on peut donner les définitions habituelles : une forme f est
dite fermée si 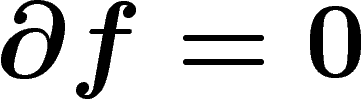 (son intégrale sur le bord d'une
partie de X sera nulle). Le
quotient des d-formes fermées par les différentielles des
(son intégrale sur le bord d'une
partie de X sera nulle). Le
quotient des d-formes fermées par les différentielles des
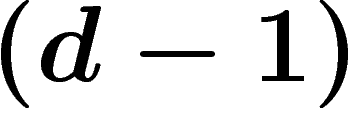 -formes est le d-ième groupe de cohomologie de De Rham
-formes est le d-ième groupe de cohomologie de De Rham
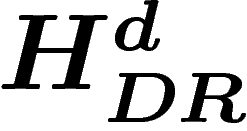 de notre variété. Par exemple, la cohomologie de De Rham du
cercle, en degré 1, est engendrée par la forme
de notre variété. Par exemple, la cohomologie de De Rham du
cercle, en degré 1, est engendrée par la forme 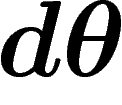 .
.
La cohomologie ainsi définie vérifie toutes les propriétés usuelles. Le
théorème de De Rham dit qu'elle est isomorphe à la cohomologie singulière
à coefficients dans 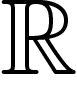 .
.
Le théorème d'isomorphisme d'Eilenberg-Steenrod. D'autres
variantes de théories cohomologiques ont été définies. Pour tous les
espaces simples, elles donnent des résultats identiques. Ceci n'est pas
un hasard : si on appelle théorie homologique une théorie qui à certaines
paires d'espaces topologiques 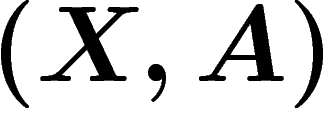 associe de manière fonctorielle et
invariante par homotopie un G-module gradué
associe de manière fonctorielle et
invariante par homotopie un G-module gradué
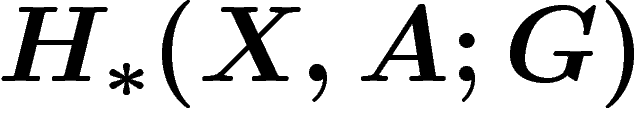 , de sorte que la suite exacte d'une paire, l'homologie du point et la propriété
d'excision soient vérifiées, alors on a :
, de sorte que la suite exacte d'une paire, l'homologie du point et la propriété
d'excision soient vérifiées, alors on a :
Soient 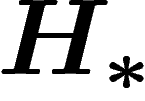 et
et 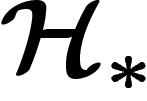 deux théories homologiques à coefficients
dans G et
deux théories homologiques à coefficients
dans G et  , et soit
, et soit 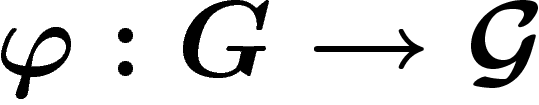 un morphisme de groupes.
Alors pour tout complexe simplicial fini X, pour tout
un morphisme de groupes.
Alors pour tout complexe simplicial fini X, pour tout  (donc pour tout espace topologique finiment triangulable), on a un unique
morphisme de modules différentiels gradués de
(donc pour tout espace topologique finiment triangulable), on a un unique
morphisme de modules différentiels gradués de 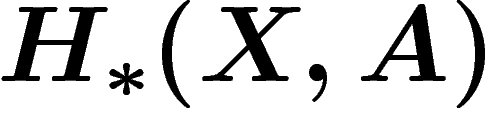 dans
dans
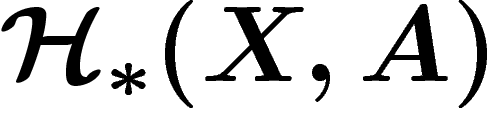 , covariant en
, covariant en 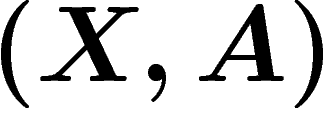 , confondu avec
, confondu avec  si
X est un point. De plus, si
si
X est un point. De plus, si  est un isomorphisme, ce
morphisme aussi.
est un isomorphisme, ce
morphisme aussi.
Ce théorème assure donc l'unicité de la théorie (co)-homologique sur les espaces finiment triangulables.
Nous présentons ici quelques exemples d'application, soit directe des théories cohomologiques existantes, soit de généralisation à partir des idées cohomologiques dans des situations différentes.
Notons que toutes les généralisations montrent clairement la supériorité de la cohomologie sur l'homologie ; les analogues homologiques de ces extensions n'existent parfois même pas. Ceci doit sans doute être attribué au fait que la cohomologie permet de tirer entièrement parti de la structure de l'espace des coefficients.
Caractéristique d'Euler et théorèmes de points fixes (exposé
de Julien Marché). Pour un polyèdre, un graphe planaire, ou une surface
triangulée, on définit depuis bien longtemps la caractéristique d'Euler
comme la somme  où S est le nombre de sommets, A le nombre
d'arêtes et F le nombre de faces. Dans le cas d'un polyèdre, cela vaut
toujours
où S est le nombre de sommets, A le nombre
d'arêtes et F le nombre de faces. Dans le cas d'un polyèdre, cela vaut
toujours  , toujours
, toujours  pour un graphe planaire ; dans le cas d'une
surface, le résultat est indépendant de la triangulation choisie, et vaut
pour un graphe planaire ; dans le cas d'une
surface, le résultat est indépendant de la triangulation choisie, et vaut
 moins
moins  fois le nombre de trous de la surface.
fois le nombre de trous de la surface.
La quantité
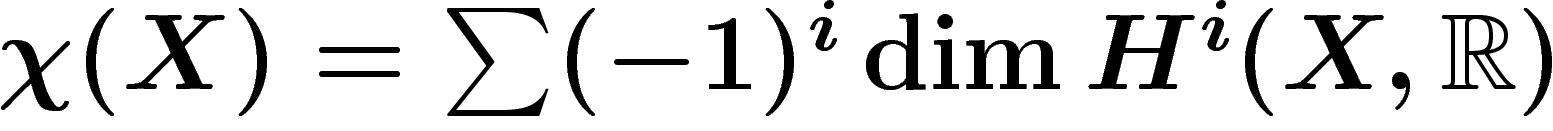 généralise la formule précédente.
Elle est reliée à de nombreuses propriétés géométriques de l'espace X.
Par exemple, le nombre des zéros d'un champ de vecteurs sur une variété,
comptés avec leur indice (nombre de fois où le champ tourne autour du
zéro en question), est égal, pour tout champ de vecteurs, à la
caractéristique d'Euler. Une formule analogue relie le nombre de points
fixes d'une application f de X dans X à la somme alternée des
traces de f sur les groupes de cohomologie.
généralise la formule précédente.
Elle est reliée à de nombreuses propriétés géométriques de l'espace X.
Par exemple, le nombre des zéros d'un champ de vecteurs sur une variété,
comptés avec leur indice (nombre de fois où le champ tourne autour du
zéro en question), est égal, pour tout champ de vecteurs, à la
caractéristique d'Euler. Une formule analogue relie le nombre de points
fixes d'une application f de X dans X à la somme alternée des
traces de f sur les groupes de cohomologie.
Cohomologie de  des faisceaux (exposé de Yann
Ollivier). À l'origine de cette théorie, on trouve des problèmes de
recollements. Si on a un recouvrement d'un espace topologique, si on a
des fonctions définies sur chaque partie du recouvrement, et si ces
fonctions se recollent bien sur chaque intersection de parties du
recouvrement, alors on peut définir un objet global sur tout l'espace,
qui sera un élément de la cohomologie de l'espace à valeurs dans notre
espace de fonctions.
des faisceaux (exposé de Yann
Ollivier). À l'origine de cette théorie, on trouve des problèmes de
recollements. Si on a un recouvrement d'un espace topologique, si on a
des fonctions définies sur chaque partie du recouvrement, et si ces
fonctions se recollent bien sur chaque intersection de parties du
recouvrement, alors on peut définir un objet global sur tout l'espace,
qui sera un élément de la cohomologie de l'espace à valeurs dans notre
espace de fonctions.
Par ailleurs, il peut être intéressant de regarder la cohomologie à
valeurs dans un espace qui pourrait varier d'un endroit à un autre. Si on
a par exemple un quotient Y d'un espace X : 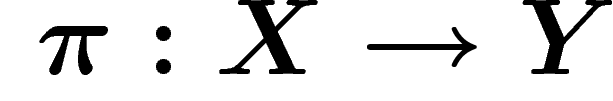 , on peut vouloir obtenir
des informations sur la cohomologie de X à partir de la cohomologie de
Y et, en tout point
, on peut vouloir obtenir
des informations sur la cohomologie de X à partir de la cohomologie de
Y et, en tout point 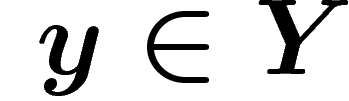 , de la cohomologie de la fibre
, de la cohomologie de la fibre
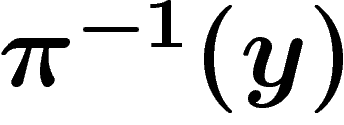 .
.
Ces considérations amènent à la définition des faisceaux. Un faisceau
 sur un espace topologique X est une application qui à chaque
ouvert U de X associe un groupe
sur un espace topologique X est une application qui à chaque
ouvert U de X associe un groupe 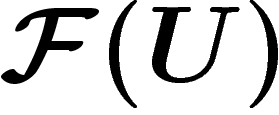 , dont les éléments sont
appelés sections au-dessus de U, en même temps qu'une
opération de restriction
, dont les éléments sont
appelés sections au-dessus de U, en même temps qu'une
opération de restriction 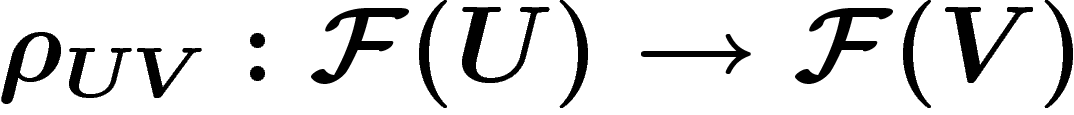 , pour
, pour  ,
vérifiant que si
,
vérifiant que si  , alors
, alors
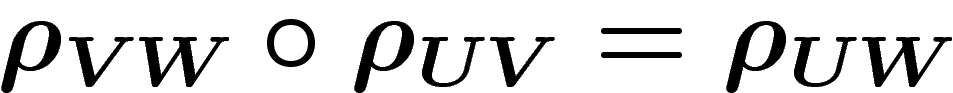 . On demande en outre deux conditions
de recollement : pour deux sections sur U et V, qui coïncident sur
. On demande en outre deux conditions
de recollement : pour deux sections sur U et V, qui coïncident sur
 , il existe une section sur
, il existe une section sur  qui se restreint sur ces
deux-là ; en outre, toute section sur
qui se restreint sur ces
deux-là ; en outre, toute section sur  dont les restrictions à
U et V sont nulles est nulle.
dont les restrictions à
U et V sont nulles est nulle.
Par exemple, l'espace des fonctions continues sur les ouverts d'un espace topologique est un faisceau.
La cohomologie classique s'interprète dans ce cadre, en prenant des fonctions localement constantes : si on recouvre un cercle par deux demi-cercles un peu élargis, si on définit une fonction localement constante sur l'intersection des deux parties (qui n'est pas connexe), elle pourra prendre deux valeurs, et il sera impossible de l'étendre en une fonction localement constante sur tout le cercle (i.e. une constante).
Ceci motive la définition de la cohomologie de  à valeurs dans un
faisceau. Soit X un espace topologique. Soit
à valeurs dans un
faisceau. Soit X un espace topologique. Soit  un
recouvrement ouvert de X. Soit
un
recouvrement ouvert de X. Soit  un faisceau sur X. On définit les
cochaînes de degré k à valeurs dans
un faisceau sur X. On définit les
cochaînes de degré k à valeurs dans  comme les applications qui à
chaque k-uplet d'ouverts du recouvrement, associent une section sur leur
intersection :
comme les applications qui à
chaque k-uplet d'ouverts du recouvrement, associent une section sur leur
intersection :
![\[
C^k(U,\F)=\prod_{i_1, \ldots, i_k} \F(U_{i_1}\cap\ldots \cap U_{i_k})
\]](cohom083.png)
On veut dire qu'une cochaîne est fermée si elle coïncide avec elle-même sur les
intersections de  ouverts. On définit donc l'opérateur bord
ouverts. On définit donc l'opérateur bord 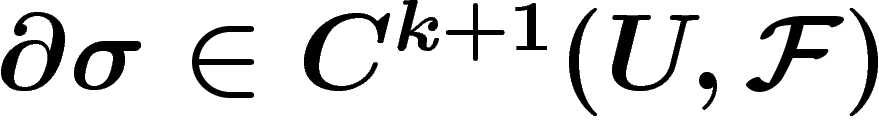 pour
pour 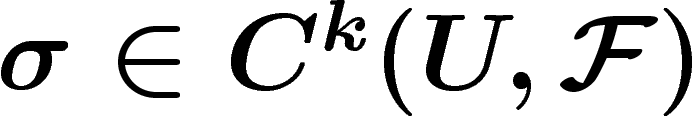 par :
par :
![\[
\d \sigma(U_{i_0},\ldots,U_{i_k})=\sum_{j=0}^k
(-1)^j\sigma(U_{i_0},\ldots,\widehat{U_{i_j}},\ldots,U_{i_k})_{|U_{i_0}\cap\ldots\cap
U_{i_k}}
\]](cohom087.png)
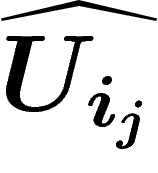 signifie qu'on retire
signifie qu'on retire 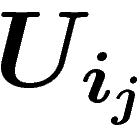 de la liste et
où
de la liste et
où  indique la restriction à V.
indique la restriction à V.
Ensuite, on dit qu'une cochaîne est fermée si son bord est nul, que c'est un cobord si c'est le bord d'une autre cochaîne, et on définit :
![\[
H^k(U,\F)=\frac{\Ker \d : C^k(U,\F) \ra C^{k+1}(U,\F)}{\Img \d :
C^{k-1}(U,\F) \ra C^k(U,\F)}
\]](cohom091.png)
Tout ceci dépend de notre choix de recouvrement. On a évidemment une
application naturelle de la cohomologie sur un recouvrement vers la
cohomologie sur un recouvrement plus fin. Ceci permet de définir
rondement la cohomologie de  de l'espace X comme la limite
inductive, sur tous les recouvrements, de la cohomologie ci-dessus. En
fait, un théorème de Leray affirme que lorsqu'on a pris un recouvrement
dont tous les éléments, ainsi que toutes leurs intersections finies, sont
contractiles, alors la limite est déjà atteinte, ce qui facilite
grandement les calculs.
de l'espace X comme la limite
inductive, sur tous les recouvrements, de la cohomologie ci-dessus. En
fait, un théorème de Leray affirme que lorsqu'on a pris un recouvrement
dont tous les éléments, ainsi que toutes leurs intersections finies, sont
contractiles, alors la limite est déjà atteinte, ce qui facilite
grandement les calculs.
La cohomologie à valeurs dans le faisceau des fonctions localement constantes se confond avec la cohomologie ordinaire (voir l'exemple du cercle ci-dessus).
La cohomologie d'un faisceau admettant des partitions de l'unité (comme le faisceau des fonctions continues sur un espace régulier) sera nulle en degré strictement positif.
La cohomologie des faisceaux contient autant d'information sur le faisceau que sur l'espace sous-jacent. Si par exemple, sur une variété, on prend comme section sur un ouvert les formes différentielles sur cet ouvert, on peut démontrer le théorème de De Rham qui indique que la cohomologie de De Rham est isomorphe à la cohomologie ordinaire, en combinant astucieusement ce qu'on met dans le faisceau et le degré de la cohomologie que l'on prend.
La cohomologie des faisceaux est extrêmement utile tant en géométrie algébrique qu'en géométrie complexe. Elle est entre autres un outil puissant d'étude des fibrés, formalisant par exemple l'intuition qu'un fibré en droites ne peut pas faire grand-chose d'autre que de tourner sur lui-même quand on parcourt une boucle non triviale de l'espace de base. Elle peut aussi servir à définir diverses classes caractéristiques.
Cohomologie des groupes (exposés de Gaëtan Chenevier et
Jérôme Plût). L'idée de base est de construire un complexe 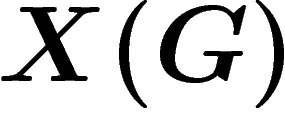 à partir d'un
groupe G de la façon suivante : les k-cellules du complexe seront
simplement les k-uplets d'éléments du groupe, l'opérateur bord étant
définie de la manière naturelle. Ceci n'apporte guère d'information sur
le groupe, aussi introduit-on une contrainte supplémentaire : on va
regarder des cochaînes, et on va imposer qu'une cochaîne soit invariante
par l'action de G sur
à partir d'un
groupe G de la façon suivante : les k-cellules du complexe seront
simplement les k-uplets d'éléments du groupe, l'opérateur bord étant
définie de la manière naturelle. Ceci n'apporte guère d'information sur
le groupe, aussi introduit-on une contrainte supplémentaire : on va
regarder des cochaînes, et on va imposer qu'une cochaîne soit invariante
par l'action de G sur 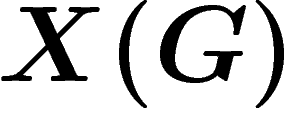 par translation (et on introduit un léger
décalage des indices afin de rester cohérent). On définit donc
par translation (et on introduit un léger
décalage des indices afin de rester cohérent). On définit donc
![\[
C^k(G,\R)=\left\{f:G^{k+1}\ra \R,\, \forall g \in
G,f(g_0,\ldots,g_k)=f(g.g_0,\ldots,g.g_k)\right\}
\]](cohom095.png)
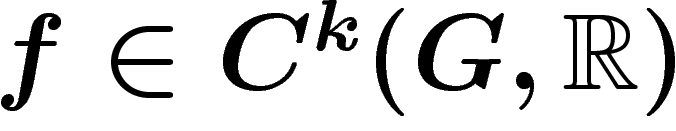 :
:![\[
(\d f)(g_0,\ldots,g_{k+1})=\sum_{i=0}^{n+1}(-1)^i
f(g_0,\ldots,\widehat{g_i},\ldots,g_{k+1})
\]](cohom097.png)
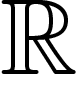 par n'importe quel groupe commutatif.)
par n'importe quel groupe commutatif.)
La cohomologie du groupe G à valeurs dans 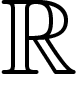 est reliée à une
cohomologie ordinaire : si X est un espace topologique contractile, que
G agit sur X librement par homéomorphismes, et que le quotient
est reliée à une
cohomologie ordinaire : si X est un espace topologique contractile, que
G agit sur X librement par homéomorphismes, et que le quotient 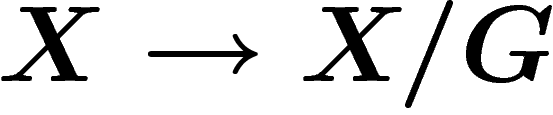 est un revêtement, alors
est un revêtement, alors 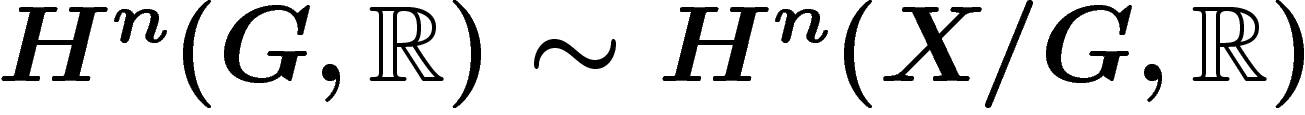 où le membre
de droite est la cohomologie ordinaire. L'espace
où le membre
de droite est la cohomologie ordinaire. L'espace 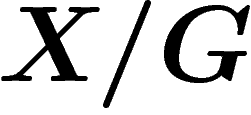 est appelé un
classifiant de G ; on peut montrer qu'il en existe toujours, et qu'il
est à peu près unique.
est appelé un
classifiant de G ; on peut montrer qu'il en existe toujours, et qu'il
est à peu près unique.
On peut généraliser encore un peu en prenant un G-module V (par exemple, une représentation de G) comme espace des coefficients, et en définissant
![\[
C^k(G,V)=\left\{f:G^{k+1}\ra V,\, \forall g \in
G,g.f(g_0,\ldots,g_k)=f(g.g_0,\ldots,g.g_k)\right\}
\]](cohom103.png)
Cette définition est utile pour l'étude géométrique des groupes infinis, cf. ci-dessous. Elle a en outre des applications en théorie des groupes finis et en théorie des nombres.
Propriété 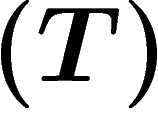 de Kazhdan et cohomologie des groupes (exposé
de François Alter). Les trente dernières années ont vu le développement de
l'étude des groupes infinis (les groupes finis étant bien balisés) d'un
point de vue géométrique. Diverses propriétés ont été définies :
moyennabilité, hyperbolicité, propriété
de Kazhdan et cohomologie des groupes (exposé
de François Alter). Les trente dernières années ont vu le développement de
l'étude des groupes infinis (les groupes finis étant bien balisés) d'un
point de vue géométrique. Diverses propriétés ont été définies :
moyennabilité, hyperbolicité, propriété 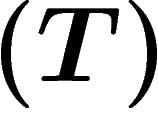 de Kazhdan... Cette dernière
est intimement reliée à la cohomologie des groupes.
de Kazhdan... Cette dernière
est intimement reliée à la cohomologie des groupes.
Parmi les innombrables définitions de la propriété 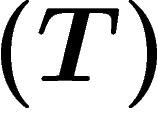 , donnons
celle-ci. Soit G un groupe (localement compact, à base dénombrable).
Soit
, donnons
celle-ci. Soit G un groupe (localement compact, à base dénombrable).
Soit 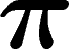 une représentation unitaire de G dans un espace de Hilbert
H (i.e. un morphisme de G dans le groupe des transformations
linéaires unitaires de H). On dit que
une représentation unitaire de G dans un espace de Hilbert
H (i.e. un morphisme de G dans le groupe des transformations
linéaires unitaires de H). On dit que 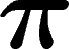 a un vecteur invariant s'il
existe un
a un vecteur invariant s'il
existe un 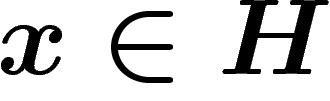 fixé par tous les éléments de G. On dit que
fixé par tous les éléments de G. On dit que 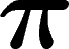 a
des vecteurs presque invariants si pour tout compact
a
des vecteurs presque invariants si pour tout compact  , pour
tout tout
, pour
tout tout 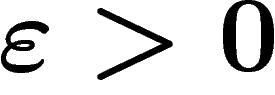 , il existe un
, il existe un 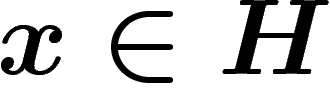 tel que les éléments de K
déplacent x de moins de
tel que les éléments de K
déplacent x de moins de  :
: 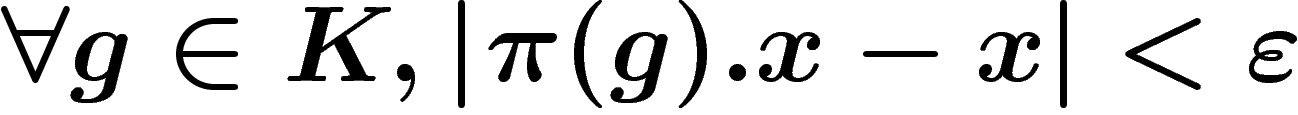 .
.
Maintenant, on dit que G est un groupe de Kazhdan (ou qu'il a la
propriété 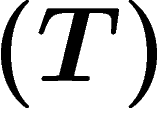 ) si toute représentation unitaire de G ayant des
vecteurs presque invariants a un vecteur invariant.
) si toute représentation unitaire de G ayant des
vecteurs presque invariants a un vecteur invariant.
Cette propriété est stable par morphisme continu (pour l'adhérence de l'image), par quotient (continu). Elle est vraie dans les groupes compacts.
Par (contre-)exemple, 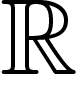 n'a pas la propriété
n'a pas la propriété 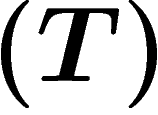 : si on prend
: si on prend 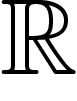 agissant sur
agissant sur 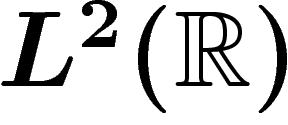 par translations, une fonction constante sur un
long intervalle est un vecteur presque invariant ; et pourtant il n'y a
pas de vecteurs invariants.
par translations, une fonction constante sur un
long intervalle est un vecteur presque invariant ; et pourtant il n'y a
pas de vecteurs invariants.
À l'inverse, il est souvent difficile de montrer que des groupes ont la
propriété 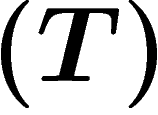 (il faut considérer toutes les représentations...). Ceci
bien qu'en un certain sens, un groupe infini ait la propriété
(il faut considérer toutes les représentations...). Ceci
bien qu'en un certain sens, un groupe infini ait la propriété 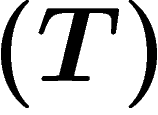 avec
une grande probabilité. Signalons quand même que
avec
une grande probabilité. Signalons quand même que 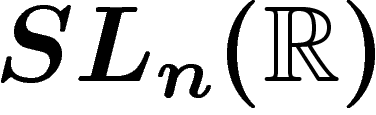 la possède
pour tout
la possède
pour tout 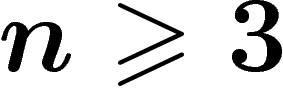 .
.
Les groupes de Kazhdan sont très loin d'être commutatifs : un groupe
de Kazhdan commutatif est compact ; l'abélianisé ![$G/\overline{[G,G]}$](cohom125.png) d'un groupe de Kazhdan est compact.
d'un groupe de Kazhdan est compact.
La propriété 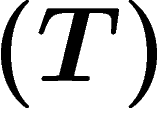 est fortement reliée à la cohomologie : un théorème
non trivial dit qu'un groupe G est de Kazhdan si et seulement si pour
toute représentation unitaire
est fortement reliée à la cohomologie : un théorème
non trivial dit qu'un groupe G est de Kazhdan si et seulement si pour
toute représentation unitaire 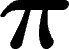 de G, le premier groupe de
cohomologie à valeurs dans
de G, le premier groupe de
cohomologie à valeurs dans 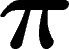 défini ci-dessus,
défini ci-dessus, 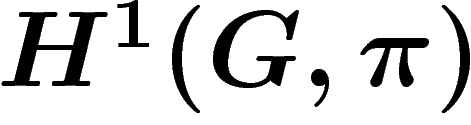 , est
nul.
, est
nul.
Pouver qu'un groupe a la propriété 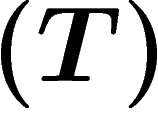 est malheureusement souvent
difficile. Elle peut parfois être obtenue par la cohomologie de certains groupes
agissant sur des ensembles combinatoires particuliers, par exemple des
immeubles (exposé de Vincent Secherre).
est malheureusement souvent
difficile. Elle peut parfois être obtenue par la cohomologie de certains groupes
agissant sur des ensembles combinatoires particuliers, par exemple des
immeubles (exposé de Vincent Secherre).
Autres cohomologies. Des généralisations voient constamment
le jour : cohomologie bornée des groupes ou des variétés (invention de
Gromov qui consiste à prendre des cochaînes réelles bornées, ce qui
permet de mettre des normes sur les groupes de cohomologie ; elle est
reliée à des invariants riemanniens des variétés, ou à des propriétés des
groupes telles que l'hyperbolicité ou la moyennabilité) ; cohomologies
équivariante, 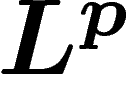 , motivique,
, motivique, 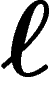 -adique, rigide, cristalline, étale...
(dont je ne connais que le nom). Signalons des applications diverses en
physique théorique (exposé de Louis Paulot). Suite du groupe de travail
l'année prochaine...
-adique, rigide, cristalline, étale...
(dont je ne connais que le nom). Signalons des applications diverses en
physique théorique (exposé de Louis Paulot). Suite du groupe de travail
l'année prochaine...