Les entropies de systèmes dynamiques

Un système dynamique est une application d'un espace dans lui-même, que l'on itère. On s'intéresse à des propriétés telles que l'existence de points fixes, périodiques, la caractérisation des orbites denses, la recherche de quantités invariantes, la divergence d'orbites partant de points proches, etc. On considère généralement que l'espace a une structure supplémentaire : une structure topologique, ou bien, en théorie ergodique, une mesure de probabilité.

L'idée de la définition de l'entropie d'un système dynamique est la suivante : on considère que la position initiale du système n'est pas connue avec une précision infinie, mais que le comportement qu'on va observer en itérant le système va nous renseigner de mieux en mieux sur le point dont on est parti (par exemple, à chaque étape, on sait dire si on se trouve dans la moitié droite ou gauche de l'espace ; dans beaucoup de cas, cette information sur l'ensemble de la trajectoire permet de reconstituer le point de départ). La quantité moyenne d'information qu'on gagne à chaque itération est l'entropie du système.

L'entropie ergodique

Soit X un espace doté d'une mesure $\mu$ de masse $1$

. Un système dynamique ergodique sur X est alors une application mesurable $T:X\rightarrow X$ préservant la mesure, c'est-à-dire que pour toute partie $A\subset X$ (mesurable), on a $\mu(T^{-1}A)=\mu(A)$ . L'application T n'est pas nécessairement inversible.

On dit que T est ergodique si toute partie de X invariante par T est de mesure soit $0$

, soit

(si ce n'est pas le cas, on décompose).

On dit que deux systèmes ergodiques $T:(X,\mu)\rightarrow (X,\mu)$ et $T':(X',\mu')\rightarrow (X',\mu')$ sont mesurablement équivalents s'il existe une bijection mesurable $\phi:X\rightarrow X'$ (modulo des ensembles de mesure nulle dans X et $X'$

) qui envoie la mesure $\mu$ sur $\mu'$ et qui envoie l'action sur l'action, i.e. $T'\circ\phi=\phi\circ T$ .

Un des principaux buts de la théorie est d'essayer de classer les systèmes ergodiques à équivalence près.

Motivation : les invariants spectraux

Von Neumann a défini toute une classe d'invariants de systèmes ergodiques : les invariants spectraux. On peut évidemment se demander si ces invariants suffisent à déterminer la dynamique à équivalence près. C'étaient les seuls invariants connus jusqu'à l'introduction de l'entropie ergodique par Kolmogorov.

L'idée est de faire agir T sur des espaces de fonctions sur X en envoyant une fonction f sur $f\circ T$ . En particulier, ceci définit un opérateur $U_T:L^2(X)\rightarrow L^2(X)$ , et comme T conserve la mesure, cet opérateur est une isométrie de $L^2(X)$

Les propriétés de cet opérateur permettent de capturer une partie du comportement du système. Par exemple, le fait que T soit ergodique est équivalent au fait que $\dim \Ker (U_T-\Id)=1$ . Le fait que T soit mélangeant (i.e. pour toutes parties $A, B\subset X$ , on a $\lim \mu(A\cap T^{-n}B)=\mu(A)\mu(B)$ ) est équivalent au fait que pour toutes fonctions $f,g\in L^2(X)$ , on a $\lim \int\! f.U_T^n g=\int\! f\,.\int\! g$ .

Dans le cas d'une matrice de 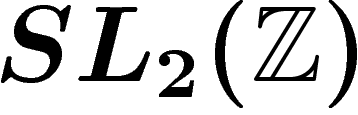$SL_2(\Z)$ agissant sur le tore $\mathbb{T}^2$ , la base de Fourier de $L^2$

permet de calculer explicitement l'opérateur. Par exemple si $A\in SL_2(\Z)$ , la transformation induite est ergodique si et seulement si le spectre de A ne contient pas de racine de l'unité, ou encore si et seulement si toutes les orbites de la transposée ${}^t\!A$ agissant sur $\Z^2$ sont infinies. On voit alors sur la base de Fourier, dans cette situation, que toutes les matrices A ergodiques seront spectralement équivalentes. Sont-elles mesurablement équivalentes ?

Une application ergodique T vérifie alors les propriétés suivantes. Si $f\in H_\lambda$ , alors le module de f est constant. De plus, pour tout $\lambda$ on a $\dim H_\lambda=1$ . Enfin, l'ensemble des valeurs propres de T est un sous-groupe dénombrable du cercle unité de $\C$ . (De plus, on peut montrer que tout sous-groupe dénombrable du cercle peut être obtenu ainsi.)

On dit que T est à spectre purement atomique si les $H_\lambda$ engendrent (au sens $L^2$

) l'espace $L^2(X)$

Von Neumann a démontré que pour des opérateurs à spectre purement atomique, la dynamique est caractérisée par les invariants spectraux :

Théorème.

Deux applications ergodiques définissant des opérateurs à spectre purement atomique sont mesurablement équivalentes si et seulement si ces opérateurs ont les mêmes valeurs propres.

À ce stade on ne sait toujours pas si les actions linéaires sur le tore sont mesurablement équivalentes. L'entropie ergodique permet de répondre à cette question.

Définition de l'entropie ergodique

Pour définir l'entropie ergodique, on se donne une partition $\mathcal{P}$ (non triviale) de X. On regarde dans quelle partie de la partition tombent les itérés $T^nx$

d'un point de départ x. L'idée est que cette suite de parties fournit de l'information sur le point x ; l'entropie est alors la quantité d'information moyenne que chaque itération de T apporte.

La suite des parties dans lesquelles tombe $T^nx$

constitue donc une sorte de code de x.

Soit $\mathcal{P}_n(x)$ l'ensemble des points $y\in X$ tels que pour tout $k\leq n$ , les points $T^kx$

sont dans la même partie de la partition $\mathcal{P}$ .

On dit que T est fortement ergodique si tous les itérés $T^n$

sont ergodiques (une application ergodique n'est pas nécessairement fortement ergodique).

On montre alors facilement que si T est fortement ergodique, alors pour tout x, la mesure $\mu(\mathcal{P}_\infty(x))$ est nulle. Autrement dit, le codage code bien. En effet, soit $Y=\mathcal{P}_\infty(x)$ et supposons $\mu(Y)>0$ . Par le théorème de récurrence de Poincaré, il existe un n tel que $\mu(Y\cap T^{-n}Y)>0$ . Soit donc $y\in Y\cap T^{-n}Y$ , alors le code de y est périodique de période n. En particulier, le code de x est périodique. Donc $Y\subset T^{-n}Y$ . Comme T conserve la mesure, on a donc $Y=T^{-n}Y$ ce qui contredit l'ergodicité de $T^n$

On voit donc que $\mu(\mathcal{P}_n(x))$ tend vers $0$

. En fait cette quantité tend exponentiellement vite vers $0$

, et l'exposant est précisément lié à l'entropie ergodique de T. On sait par la théorie de l'information que donner le code de x dans la partition jusqu'à l'étape n, c'est donner une quantité d'information $-\log \mu(\mathcal{P}_n(x))$ . Ceci est précisé par le théorème-définition suivant, énoncé d'abord par Shannon :

Théorème.

Soit $T:X\rightarrow X$ une application préservant la mesure $\mu$ . Soit $\mathcal{P}$ une partition de X telle que

$-\sum_{P\in \mathcal{P}} \mu(P)\log \mu(P)<\infty$

Alors la limite

$h(T,\mathcal{P},x)=-\lim_{n\rightarrow\infty} \frac1n\log \mu(\mathcal{P}_n(x))$

existe pour $\mu$ -presque tout x, et cette quantité, en tant que fonction de x, converge dans $L^1(X)$

vers une fonction T-invariante.

En particulier, si T est ergodique, l'entropie ne dépend pas de x. Sinon, on moyenne en posant $h(T,\mathcal{P})=\int_X h(T,\mathcal{P},x)d\mu(x)$ . Ensuite, on remarque que l'entropie augmente lorsqu'on raffine la partition, on pose donc :

Pour $A\in SL_2(\Z)$ agissant sur le tore, on peut montrer que cette entropie est égale au log du module de la plus grande valeur propre. En particulier, toutes les matrices ergodiques ne sont pas mesurablement équivalentes.

Pour le décalage de Bernoulli, sur un alphabet $\{a_1,\ldots,a_m\}$ , considérons la partition $\mathcal{P}=\{P^k\}$ où $P^k=\{(x_0,x_1,\ldots), x_0=a_k\}$ . On peut raffiner cette partition par le décalage, cela revient à fixer les n premières lettres, on obtient ainsi des partitions arbitrairement fines. L'entropie de ces partitions se calcule facilement : on a $\mathcal{P}_n(x)=\{(y_0,y_1,\ldots), x_i=y_i\text{ pour tout }i\leq n\}$ . Si $p_k$

est la probabilité d'occurrence de la lettre k, la mesure de l'ensemble $\mathcal{P}_n(x)$ vaut alors simplement $\prod_{i=0}^n p_{x_i}$ . On a donc $-\frac1n \log \mu(\mathcal{P}_n(x))=-\frac1n\sum \log p_{x_i}$ . Or, pour presque tout x, la proportion des $x_i$

qui sont égaux à la lettre $a_k$

est, d'après la loi des grands nombres, $p_k$

. La quantité $-\lim_n\frac1n\sum \log p_{x_i}$ vaut donc, pour $\mu$ -presque tout x :

En fait, un théorème difficile d'Ornstein affirme que deux décalages de Bernoulli (même sur des alphabets n'ayant pas le même nombre de lettres !) sont mesurablement équivalents si et seulement s'ils ont la même entropie. Ce théorème, combiné à un autre de Katznelson qui affirme que toute application de $SL_2(\Z)$ agissant sur le tore est mesurablement équivalente à un décalage de Bernoulli (indexé par $\Z$ ), permet de traiter aussi le cas du tore.

L'entropie topologique

Définitions

On se place désormais dans un cadre métrique plutôt que mesuré. Soit donc $(X,\dist)$ un espace métrique compact, et $f:X\rightarrow X$ une application continue. La théorie de l'entropie topologique que l'on développe alors est due à Adler, Konheim, McAndrew.

L'idée est là encore qu'on ne peut séparer les points qu'avec une certaine précision, et qu'on espère que l'observation des trajectoires des points par f nous renseignera sur leur position initiale.

Soit donc $\eps>0$ . On dit que deux points $x,y\in X$ sont $\eps$ -séparés si $\dist(x,y)>\eps$ . On dit que x et y sont $\eps$ -séparés en temps n s'il existe un $k\leq n$ tel que $\dist(f^kx,f^ky)>\eps$ . Ceci amène naturellement à définir la distance

Plus n est grand, plus on sépare de points. Soit $H(n,\eps)$ le nombre maximum de points d'une famille de points deux à deux $(n,\eps)$ -séparés. Combinatoirement, identifier l'un de ces points est donner une information $\log H(n,\eps)$ . On définit l'entropie topologique de f par

On aurait pu donner une variante de cette définition en posant pour $H(n,\eps)$ le nombre minimal de boules de rayon $\eps$ pour $\dist_n$ recouvrant tout X. On trouve la même entropie.

Une autre manière de voir est de considérer le graphe $\Gamma_k=\{(x,fx,\ldots,f^kx)\}\subset X^{k+1}$ et de compter le nombre de pavés de côté $\eps$ nécessaires pour le recouvrir.

Comme X est compact, deux métriques quelconques donnant la même topologie sont uniformément équivalentes. Cela implique que l'entropie définie ci-dessus ne dépend pas de la métrique choisie, d'où son qualificatif de topologique.

$h_{top}(f)=\sup\{h(f,\mu), \mu\text{ mesure de probabilité }f\text{-invariante sur }X\}$

On peut de plus montrer que si f est un difféomorphisme $C^\infty$ d'une variété, ce sup est atteint.

Premier exemple : l'entropie d'une rotation du cercle est nulle, comme celle de toute isométrie.

L'entropie de l'application du cercle unité de $\C$ définie par $z\mapsto z^2$ est égale à $\log 2$ : en effet on a $\dist_n=2^n\dist$ , on sépare deux fois mieux les points à chaque itération. De manière plus générale, l'entropie de $z\mapsto z^k$ sur le cercle est égale à $\log k$ .

Soit la matrice $\left(\begin{matrix}2&1\\1&1\end{matrix}\right)$ agissant sur le tore $\mathbb{T}^2$ . On a une valeur propre dilatante $\frac{3+\sqrt{5}}{2}$ , et une étude locale montre que l'entropie est égale au log de cette valeur.

De manière générale, si un système dynamique (ou l'un de ses itérés) possède une figure topologiquement équivalente à un « fer à cheval », c'est-à-dire un carré dont l'image par f l'intersecte deux fois (dans la bonne direction), alors l'entropie topologique sera strictement positive.

En effet dans cette situation, on a un ensemble limite composé d'une infinité de bandes dans le carré, et spécifier un point sur une bande demande de spécifier, pour chaque étape, si on choisit la partie haute ou la partie basse.

Inversement, un théorème de Katok affirme que si f est un difféomorphisme $C^\infty$ d'une surface compacte, d'entropie strictement positive, alors f ou l'un de ses itérés possède un fer à cheval.

Entropie topologique et entropie algébrique

Dans cette situation, on peut définir d'autres invariants à l'aide de l'idée d'entropie. L'un d'eux est l'entropie algébrique.

Soient X une variété compacte lisse et f une application $C^{\infty}$ . Elle induit un morphisme sur le groupe fondamental de X, soit $f_\ast:\pi_1(X)\rightarrow \pi_1(X)$ . (Mettons pour simplifier qu'il existe un point périodique, qu'on prend comme point-base du $\pi_1$ .)

Le groupe fondamental $\pi_1(X)$ est engendré par une partie génératrice $S=\{a_1,\ldots,a_k\}$ (on prend S symétrique, c'est-à-dire que S contient les inverses de ses éléments), ces éléments vérifiant certaines relations. Alors, tout élément du $\pi_1$ peut être écrit comme un produit d'éléments de S. On définit la longueur $\ell(x)$ d'un élément $x\in\pi_1(X)$ comme le nombre minimal d'éléments de S qu'il faut pour l'écrire.

$h_{\pi_1}(f)=\vlimsup_{n\rightarrow\infty} \frac1n\log \max_{1\leq i\leq k} \ell(f_\ast^n a_k)$

L'entropie ne dépend pas du système S de générateurs choisi. Cela se voit en regardant la longueur des éléments d'une nouvelle partie génératrice par rapport à l'ancienne, et en utilisant la relation $\ell(xy)\leq \ell(x)+\ell(y)$ .

De même, cette entropie est invariante par automorphisme intérieur du $\pi_1$ (conjugaison par un certain élément), ce qui implique que cette définition ne dépend pas du point-base choisi.

Un théorème de Manning précise le rapport entre entropie topologique et entropie algébrique :

Théorème.

Soit f une application $C^\infty$ sur une variété lisse. Alors

$h_{top}(f)\geq h_{\pi_1}(f)$

A priori, l'action sur le groupe fondamental ne capture donc qu'une partie de la complexité de la dynamique.

On peut travailler sur l'homologie comme sur le groupe fondamental. L'application f définit un opérateur sur l'homologie $f_\ast : H_\ast(X,\Z)\rightarrow H_\ast(X,\Z)$ . L'analogue de l'entropie algébrique est alors le log du rayon spectral $\rho(f_\ast)=\vlimsup\norm{f_\ast^n}^{1/n}$ (comparer avec le cas d'une application linéaire sur le tore), et on a un analogue, dû à Yomdin, du théorème de Manning :

Théorème.

Soit $f:X\rightarrow X$ un difféomorphisme $C^\infty$ d'une variété lisse, et soit $\rho$ le rayon spectral de $f_\ast$ , alors

$h_{top}(f)\geq \log \rho = \lim \frac1n \log \norm{f_\ast^n}$

Si X est de dimension n, on peut simplement restreindre $f_\ast$ à l'homologie en degré n de X, soit $H_n(X,\Z)\simeq \Z$ . Le rayon spectral correspondant est alors simplement le degré topologique d de f, et on a le théorème suivant :

Théorème.

Soit $f:X\rightarrow X$ une application $C^1$

sur une variété lisse, de degré d. Alors

$h_{top}(f)\geq \log d$

Attention, l'hypothèse de régularité $C^1$

est nécessaire ! Par exemple sur $\C$ , si on considère l'application donnée en coordonnées polaires par $\rho e^{i\theta} \mapsto \frac12 \rho e^{2i\theta}$ , son degré est $2$

, mais toutes les orbites tendent vers $0$

donc l'entropie est nulle. Bien sûr, cette application n'est pas $C^1$

...

L'idée de la preuve est la suivante : on prend un point et on regarde l'ensemble de ses préimages par f au temps n, il y en a $d^n$

pour un point typique. L'hypothèse de régularité $C^1$

intervient pour dire que tous ces points sont bien séparés (par exemple s'il n'y a pas de point critique, le jacobien est uniformément minoré).

Dynamique holomorphe

L'entropie algébrique ne capture donc en général qu'une partie de la complexité d'un système. On peut se demander dans quels cas on a égalité.

Soit f une application polynomiale du plan complexe complété par un point à l'infini : $f:\C\mathbb{P}^1\rightarrow\C\mathbb{P}^1$ . Par exemple, $f:z\mapsto z^2+c$ ... Soit d le degré du polynôme, c'est aussi le degré topologique de f et on sait donc que $h_{top}(f)\geq \log d$ . Un théorème de Gromov pose l'égalité :

Théorème.

Soit f une application polynomiale de $\C\mathbb{P}^1$ dans lui-même, de degré d. Alors

$h_{top}(f)=\log d$

L'idée de la preuve est de regarder le graphe $\Gamma_k=\{(x,fx,f^2x,\ldots f^kx)\}\subset \left(\C\mathbb{P}^1\right)^{k+1}$ . On cherche à évaluer le nombre $H'(k,\eps)$ de pavés de taille $\eps$ qu'il faut pour le recouvrir. L'aire de $\Gamma_k$ est supérieure à ce nombre fois la « densité minimale » de $\Gamma_k$ dans un pavé de taille $\eps$ , c'est-à-dire la plus petite surface qu'on peut y mettre. Or l'aire de $\Gamma_k$ est calculable par des moyens homologiques, et la densité minimale se trouve être négligeable, ce qui permet d'arriver au résultat.