Back to: Main Page > Économie, Politique
Étude d'un mécanisme de prix variables selon les individus
Application à différents problèmes économiques : retraites, impôts,
pénuries...
Résumé :
On considère un système où un client paye un prix proportionnel au
prix affiché par le vendeur et à un coefficient propre au client. On
établit d'abord la viabilité théorique de ce système et l'existence
d'un prix d'équilibre. Ensuite, on montre comment un tel système, avec
des coefficients bien ajustés, appliqué à des marchés relevant du
service public, peut combiner la même justice sociale que le système
actuel (quoi qu'on en pense) et la même efficacité économique qu'un
système privé concurrentiel ainsi que tous ses autres avantages (quoi
qu'on en pense également), en assurant l'équilibre. On donne quelques
applications possibles, comme le problème des retraites ou du
financement de la santé publique.
Présentation du mécanisme, étude théorique
On considère un marché de plusieurs biens sur lequel interviennent
différents individus. On suppose que chaque vendeur affiche un prix
p pour un produit qu'il vend, mais que le client, au lieu de payer
le prix p, paie une somme proportionnelle à p, le coefficient de
proportionnalité étant fonction de l'acheteur et du type de produit
acheté ; mais un même acheteur acquérant un même produit chez un autre
vendeur paiera avec le même coefficient de proportionnalité.
On appellera coefficients de paiement ces quantités. On parlera
de marché à prix modulés pour désigner ce système, par opposition aux
prix uniformes.
C'est le cas, par exemple, lorsque certains clients ont des réductions
(étudiants, familles nombreuses). Mais les mécanismes de type carte de
fidélité n'entrent pas dans cette catégorie, car le taux de remise
dépend du vendeur.
On se propose d'étudier le comportement d'un tel marché.
Cadre de l'équilibre général : existence d'un prix
d'équilibre
On se place dans le cadre de l'équilibre général : on a des individus
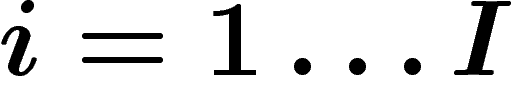 , et des biens
, et des biens 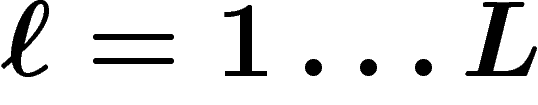 . Chaque individu i
possède un budget
. Chaque individu i
possède un budget  . Le bien
. Le bien 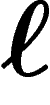 est présent sur le marché en
quantité
est présent sur le marché en
quantité 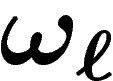 . On suppose que le
prix du bien
. On suppose que le
prix du bien 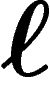 sur le marché est
sur le marché est 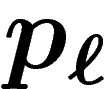 . On convient que l'individu
i, voulant acquérir une unité du bien
. On convient que l'individu
i, voulant acquérir une unité du bien 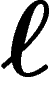 , paie non pas
, paie non pas 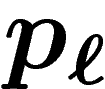 mais
mais 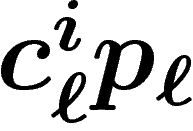 ,
, 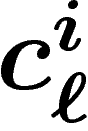 étant un nombre dépendant de
l'acheteur et du type de bien acheté (mais pas du vendeur).
étant un nombre dépendant de
l'acheteur et du type de bien acheté (mais pas du vendeur).
Chaque individu i a ainsi une fonction de demande
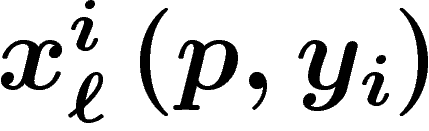 en les biens
en les biens 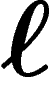 . La demande globale
en bien
. La demande globale
en bien 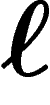 est
est 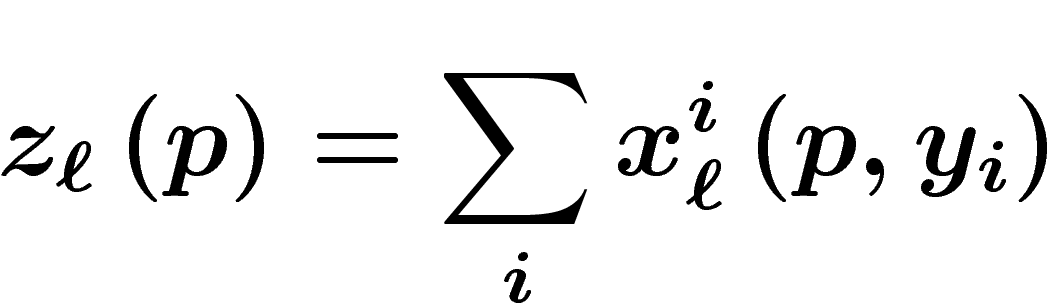 . Le marché est en équilibre si la demande
est égale à l'offre :
. Le marché est en équilibre si la demande
est égale à l'offre : 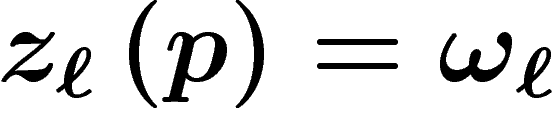 .
.
On demande s'il existe un système de prix tel que le marché est en
équilibre. Dans le cas classique du marché à prix uniformes,
la réponse est bien connue et positive sous quelques
hypothèses (préférences continues, strictement croissantes et
strictement convexes). On peut montrer (cf. annexe) qu'il en est de
même pour le cas des prix modulés, avec exactement les mêmes
hypothèses, et que comme dans le cas classique, l'allocation qui
résulte de ces prix est optimale (au sens de Pareto). Le prix
d'équilibre peut être atteint par le même type de mécanismes.
Comportement dans un cadre concurrentiel
Un tel système est-il viable dans un cadre concurrentiel ? Chaque
vendeur affiche un prix, et chaque client paye le prix indiqué par le
vendeur multiplié par son coefficient de paiement. Précisons par
avance que l'on n'entend pas appliquer ce système à des produits de
consommation courante.
Si on suppose que les clients (ou les vendeurs) sont mobiles, alors
chaque client se dirigera vers le vendeur qui lui réclame le plus faible
paiement. Comme le coefficient de paiement du client est indépendant
du vendeur, le client se dirigera simplement vers le vendeur qui
affiche le plus faible prix. Ainsi, le mécanisme de baisse des prix
par la concurrence agira comme dans le cas des prix uniformes.
Supposons une mobilité réduite. L'efficacité du mécanisme classique de
prix n'est alors pas du tout assurée. On peut craindre que le marché à
prix modulés ne fasse pire : dans des zones du marché où les clients
se trouvent avoir de faibles coefficients de paiement, les vendeurs
seront obligés d'augmenter leurs prix. Mais de toute façon, un vendeur
qui se trouve face à une clientèle qui a un coefficient de paiement
trop bas augmentera ses prix de manière à compenser exactement la
moyenne du coefficient de paiement parmi ses clients. Cela aura
peut-être pour conséquence de faire fuir les rares clients à
coefficient de paiement élevé qu'il lui restait encore.
Mais dans le pire des cas, on aboutit simplement à une ségrégation des
clients selon le coefficient de paiement, chaque vendeur ne recevant
que des clients ayant un même coefficient de paiement et ajustant ses
prix en conséquence : dans le pire des cas, on se retrouve
exactement avec un marché à prix uniformes.
Pour fixer les idées, supposons (comme ce sera le cas dans les
applications proposées) que les coefficients de paiement augmentent
avec la richesse du client (qu'il s'agisse d'un individu, d'une
entreprise...). De plus, supposons que la mobilité n'est pas parfaite,
mais quand même pas nulle. Très souvent, la mobilité des personnes
aisées est largement supérieure à celle des personnes plus pauvres. Un
vendeur qui se plaint d'avoir une clientèle pauvre peut donc
rapidement, si la clientèle aisée est assez mobile, l'attirer en
proposant des prix inférieurs à ceux de ses concurrents, ce qui
rétablira son équilibre financier.
D'autre part, la modulation des prix a pour effet que la part de
chiffre d'affaires représentée par les clients plus aisés est plus
importante que dans le cas des prix uniformes. Si on suppose que les
clients aisés sont plus mobiles que les clients moins aisés, cela a
pour effet d'augmenter la part de marché qui est mobile. Par
conséquent, en cas de mobilité imparfaite, la mobilité globale
est plus grande avec les prix modulés qu'avec les prix uniformes, et
par conséquent le mécanisme de baisse des prix par la
concurrence est plus efficace.
Marchés auxquels un tel mécanisme devrait s'appliquer
Budgets de positionnement
Théoriquement, il serait souhaitable de moduler les prix sur tous les
marchés qui ne sont pas destinés à la consommation (des ménages) ou à
la production (finale ou intermédiaire des entreprises), mais à
l'entrée sur le marché. On part donc de la considération théorique que
l'entrée sur le marché ne fait pas vraiment partie du produit
vendu*, et qu'on recherche l'égalité des moyens
d'accès au marché, afin qu'une personne (entreprise, individu)
proposant un produit plus performant (meilleur produit, meilleur
travail) puisse avoir un accès au marché égal à ceux qui sont déjà
installés.
Moduler les prix, mais comment exactement ? On peut considérer que le
détail de la modulation doit être fixé par la loi en fonction de la
situation économique et sociale (et aussi politique) ; on donnera
quand même quelques indications schématiques.
On divise le budget des ménages en deux catégories : une partie de
consommation courante et une partie concernant la manière dont ce
ménage se place sur le marché du travail. Cette dernière comprend une
part des dépenses de transport, d'éducation et de santé, à savoir la
part qui ne résulte pas d'une volonté d'accroissement du bien-être
personnel mais d'une nécessité pour travailler. Plus généralement,
cette partie comprend une bonne part de ce qui est actuellement fourni
par les services publics, et financé collectivement par l'impôt. On
appellera cette part du budget budget de positionnement, et
produits de positionnement les produits correspondants.
On considère alors que la capacité de positionnement d'un individu
doit être indépendante de son revenu. Plus exactement, on part de
l'hypothèse que la quantité de produit de positionnement qu'un
individu peut obtenir doit être la même pour deux individus qui
consacrent la même proportion de leur bien-être (de leur temps,
de leur revenu...) au budget de positionnement*. Cependant, on laisse
à chaque individu toute latitude pour consacrer un budget plus ou moins
grand à son positionnement, et pour fixer la manière optimale de
répartir ce budget entre différents postes, ce qui a l'avantage de
laisser les individus rechercher la combinaison la plus efficace
compte tenu de ce qu'ils veulent obtenir.
Ceci dit, quelle doit être la valeur des coefficients de paiement dans
un tel système ? On propose ici une réponse dans un cadre très
simplifié. On évalue, en fonction du revenu r d'un ménage, la part
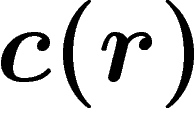 qu'il consacre à la consommation et à l'accroissement de son
bien-être, et la part
qu'il consacre à la consommation et à l'accroissement de son
bien-être, et la part 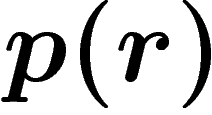 consacrée au positionnement. On prend la
valeur moyenne de ces quantités pour les ménages dont le revenu est
r. On ne veut pas toucher aux budgets de consommation, mais égaliser
les budgets de positionnement. Alors, on obtient immédiatement que le
coefficient de paiement d'un ménage ayant un revenu r doit être
consacrée au positionnement. On prend la
valeur moyenne de ces quantités pour les ménages dont le revenu est
r. On ne veut pas toucher aux budgets de consommation, mais égaliser
les budgets de positionnement. Alors, on obtient immédiatement que le
coefficient de paiement d'un ménage ayant un revenu r doit être  pour les produits de consommation (on ne change rien) et
pour les produits de consommation (on ne change rien) et 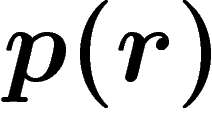 pour
les produits de positionnement (il paie plus s'il gagne plus, pas
proportionnellement à son revenu mais proportionnellement à la part de
son revenu qu'il consacrait auparavant à son positionnement).
pour
les produits de positionnement (il paie plus s'il gagne plus, pas
proportionnellement à son revenu mais proportionnellement à la part de
son revenu qu'il consacrait auparavant à son positionnement).
Répétons que ce système n'influe pas sur les biens de consommation
et la recherche du bien-être, garantit l'égalité des chances, laisse
chacun décider de l'emploi optimal des différentes ressources dont il
dispose, garantit une offre concurrentielle et ne nécessite pas
d'administration centrale.
De manière symétrique, les entreprises ont aussi un budget de
positionnement, qui contient tout ce que l'entreprise fait qui n'est
pas lié (directement ou indirectement) à l'élaboration du produit
qu'elle vend, mais à la manière de réussir sur le marché. Si on
considère que dans un fonctionnement optimal la réussite d'une
entreprise ne devrait dépendre que de la qualité du produit qu'elle
vend (en fonction des souhaits du marché), et non d'autres facteurs,
on aboutit à la conclusion que la capacité de positionnement devrait
être plus indépendante de la taille de l'entreprise. Ceci inclut par
exemple les frais de publicité ou de protection de la propriété industrielle.
Certains services publics
Une partie de l'économie correspondant aux services publics pourrait
passer aux prix modulés : grâce à la modulation des prix selon les
individus, cela peut se faire de manière à conserver la même
répartition des coûts (la même justice sociale) entre individus. Avec
ce type de mécanisme, la proximité du paiement serait récupérée
(habituellement, le consommateur oublie qu'une plus grande utilisation
de service public augmente les charges communes), tout en conservant
le principe « paiement selon les moyens » qui est le principe de
fonctionnement d'un service public. Des produits facturés ainsi
peuvent l'être par des entreprises indifféremment publiques ou
privées. Ce système combine 1) le principe de concurrence : s'il y a
plusieurs fournisseurs, les clients vont chez le moins cher ; 2) la
nécessité de justice sociale ; 3) le principe que le consommateur paye
directement pour ce qu'il consomme (ce que le service public financé
par impôt ne permet pas, et qui pourrait modèrer la demande) ; 4) ce
système ne nécessite pas d'administration centralisée. Ceci pourrait
être une instauration réaliste de l'« économie sociale » bénévole
réclamée par certains.
Mais tous les services publics ne doivent pas subir ce traitement :
par exemple dans le cas de l'éducation, si l'État prétend
officiellement favoriser l'instruction de tous, il doit éviter le
laisser à chacun (aux parents) le soin de décider de la quantité d'instruction
élémentaire qu'il reçoit, car même à bas prix certains choisiraient de
ne pas en utiliser car ils n'en voietn pas l'intérêt.
De manière générale, les services publics pour lesquels le bénéfice
n'apparaît pas immédiatement et qui existent à cause de leur intérêt
général à long terme doivent absolument être tenus à l'écart du
mécanisme de prix modulés.
Applications pratiques
Retraites
Il est tout à fait possible d'imaginer un système de retraite ayant
exactement le même niveau de justice sociale que le système par
répartition actuel, et exactement le même niveau d'efficacité que les
systèmes privés que l'on tend à développer (fonds de pension...), quoi
qu'on pense par ailleurs de celui-ci ou de celui-là.
Il suffit pour cela de prendre un système supposé plus efficace que le
système par répartition, et de le faire basculer en économie à prix
modulés, en ajustant les coefficient s de paiement des individus de
telle sorte qu'avec le même niveau de cotisation que dans le système
par répartition, un individu obtienne le même niveau de retraite : on
prend comme coefficient de paiement pour un individu sa cotisation
dans le système par répartition divisée par la retraite qu'il
obtiendrait dans ce système.
Cela laisse en outre aux individus la possibilité de moduler leurs
cotisations selon leurs souhaits.
Santé
Le système de santé fonctionne déjà en prix modulés, mais
indirectement, c'est-à-dire qu'il est financé par divers impôts.
On ne peut évidemment pas faire passer l'ensemble du système de santé
sur un système à prix modulés, car les prix modulés supposent que
l'individu est responsable de sa consommation et la choisit, alors que
ce n'est évidemment pas le cas pour les maladies, qui arrivent
aléatoirement, et que même en prix modulés, le coût du traitement
serait de toute façon énorme pour beaucoup de maladies graves.
Cependant, pour la médecine courante (consultations de généralistes
par exemple), on peut très bien instaurer des prix modulés, ce qui
aurait l'avantage de conserver la justice sociale tout en récupérant
la proximité du paiement pour le client, et pourrait limiter certains
abus. Cela reviendrait à mettre en place des tickets modérateurs
proportionnels à la richesse du client.
Publicité
Jusqu'ici nous nous sommes principalement intéressés aux ménages ;
passons aux entreprises. L'équivalent du positionnement sur le marché
du travail est alors le positionnement sur le marché d'un produit. La
publicité intervient de manière importante dans ce positionnement.
On part de la considération que l'accès à l'information du client
ne devrait pas trop dépendre de la position dominante d'une entreprise,
afin de favoriser l'émergence d'entreprises innovantes. En
modulant le prix de la publicité par le chiffre d'affaires de
l'entreprise cliente, on obtient un système qui laisse leur place aux
nouvelles entreprises.
Ceci n'impliquerait évidemment aucun changement chez les publicistes,
la publicité restant un secteur concurrentiel.
Brevets
Toujours concernant les entreprises (et dans une moindre mesure les
individus), la protection de la propriété industrielle est aussi un
sujet qui relève du positionnement d'une entreprise sur le marché, et
non du produit que fabrique l'entreprise. Le dépôt de brevets coûte
cher, et les entreprises les plus petites doivent parfois y renoncer.
L'idéal serait que le dépôt d'un brevet soit gratuit (la propriété
industrielle ou intellectuelle est un droit, pas un produit à
acheter), mais le dépôt et la protection du brevet ont un coût, et la
gratuité entraînerait des abus. L'instauration de prix modulés en
fonction du chiffre d'affaires de l'entreprise résoudrait ces
problèmes. On peut proposer le barême suivant, qui s'inspire des mêmes
principes que celui proposé plus haut pour les ménages : le
coefficient de paiement d'une entreprise serait égal à la moyenne du
budget que les entreprises ayant le même chiffre d'affaires consacrent
actuellement à la protection de la propriété industrielle.
Dans le même ordre d'idées, on pourrait aussi envisager que les
avocats et autres les frais de justice soient payés par prix modulés.
À noter que les individus déposent aussi des brevets, et qu'un barême
devrait aussi leur être appliqué, barême probablement différent de
celui des entreprises.
Pénuries
Signalons une autre application possible (assez marginale dans les pays
développés) : les situations de pénurie. Dans ces situations
(sécheresse, etc.), on décide en général d'attribuer une part fixe de
ce qui est disponible à chaque individu. Cette méthode prend pas en
compte la variabilité individuelle des besoins en ce produit :
certains pourront s'en passer plus facilement que d'autres. Pour
conserver l'aspect équitable de la répartition, on pourrait répartir
le bien en pénurie par un mécanisme de marché, chacun payant
proportionnellement à sa richesse, et le prix de base étant fixé de
manière à maintenir la demande au niveau nécessaire. Ainsi on aurait
une véritable répartition selon l'intérêt que chacun porte au produit.
Conclusion
Ce système permet donc de conserver la justice sociale
tout en gagnant tous les avantages d'une économie de marché
(concurrence, ajustement de la demande selon les besoins, absence
d'administration, paiement immédiat de ce qui est consommé...).
En pratique, il peut facilement être mis en place (en se rappelant
qu'il ne s'agit pas de l'étendre aux biens de consommation courante) :
les coefficients de paiement d'un individu pourraient par exemple être
stockés sur une carte bancaire (ce qui en garantirait la
confidentialité), et ajustés une fois tous les ans ou tous les deux
ans en prenant comme base la déclaration de revenus. Le choix précis
des coefficients de paiement relèverait de l'orientation politique,
comme actuellement la détermination des diverses impositions.
Annexe : théorème d'existence des prix d'équilibre
On se place dans le cadre de l'équilibre général : on a des individus
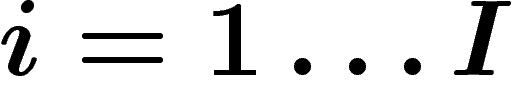 , et des biens
, et des biens 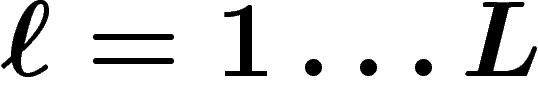 . Le bien
. Le bien 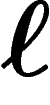 est
présent sur le marché en quantité
est
présent sur le marché en quantité 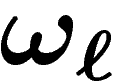 .
.
On note 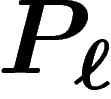 le prix du bien
le prix du bien 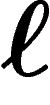 sur le marché. On décide qu'un
individu i, voulant acquérir une unité du bien
sur le marché. On décide qu'un
individu i, voulant acquérir une unité du bien 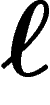 , paie non pas
, paie non pas
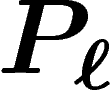 mais
mais 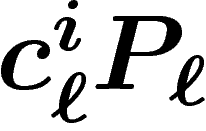 .
.
Dans le cas des prix modulés, on n'a pas de normalisation des prix,
contrairement au cas classique. On notera 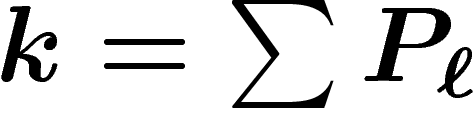 et
et
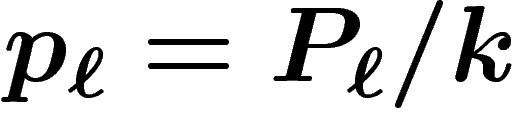 . On a ainsi
. On a ainsi 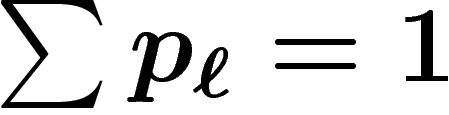 , et les prix sont
caractérisés par le couple
, et les prix sont
caractérisés par le couple 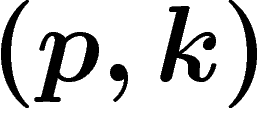 où p est normalisé.
où p est normalisé.
Soit 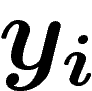 le budget de l'individu i. Soit
le budget de l'individu i. Soit
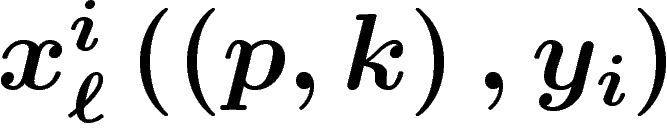 sa fonction de demande en
le bien
sa fonction de demande en
le bien 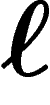 quand les prix sont
quand les prix sont 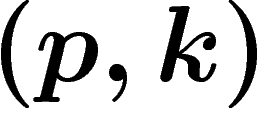 (c'est la même
que la fonction de demande habituelle quand on remplace
(c'est la même
que la fonction de demande habituelle quand on remplace
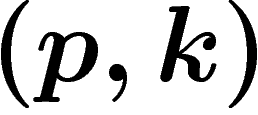 par le vecteur-prix
par le vecteur-prix 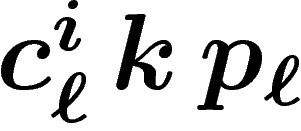 ).
).
La demande excédentaire agrégée en bien 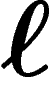 est
est 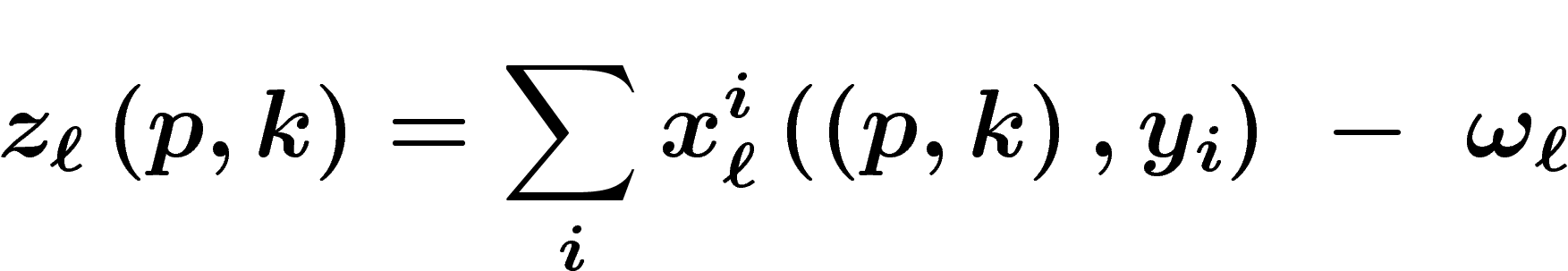 . Le marché du bien
. Le marché du bien 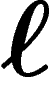 est en équilibre si et seulement si la demande est égale à l'offre :
est en équilibre si et seulement si la demande est égale à l'offre :
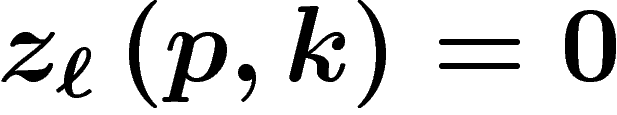 .
.
On cherche un système de prix tel que le marché de tout bien soit en
équilibre.
On se place dans le cadre habituel de préférences continues,
strictement croissantes, strictement convexes. Le théorème de Walras
(un individu utilise tout le budget dont on dispose) s'écrit pour tout
i :
![\[\sum_\ell k\, p_\ell c_\ell^i \,
x_\ell^i\left(\left(p,k\right),y_i\right)=y_i
\]](prix044.png)
(La démonstration du théorème de Walras se place dans le cadre de la
théorie du choix rationnel d'un individu soumis à un certain système
de prix; changer les rapports entre les prix payés par différents
individus ne change rien, puisque dans les prix modulés, l'individu
i est soumis au vecteur-prix 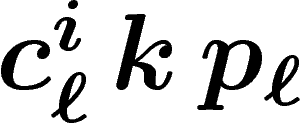 .)
.)
On va utiliser le produit scalaire 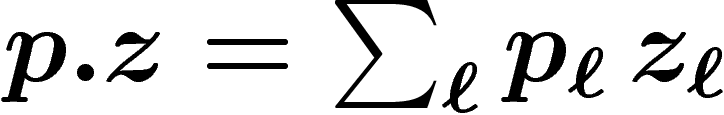 .
.
Soient
![\[k_1=\frac{1}{\min_{i,\ell}c^i_\ell} \frac{\sum_i y_i}
{\min_\ell \omega_\ell}
\ \mbox{ et } \ k_2=\frac{1}{\max_{i,\ell}c^i_\ell} \frac{\sum_i
y_i}{\max_\ell
\omega_\ell}\]](prix047.png)
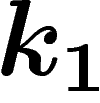 et
et 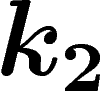 sont construits de telle sorte que si
sont construits de telle sorte que si 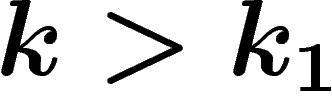 , on a
automatiquement
, on a
automatiquement  (les prix sont trop élevés) et que si
(les prix sont trop élevés) et que si 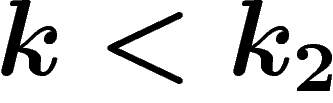 ,
on a
,
on a 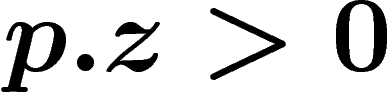 (les prix sont trop bas).
(les prix sont trop bas).
Soit E l'ensemble des couples 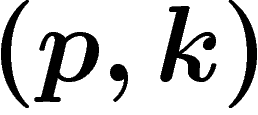 où p est un prix normé
(
où p est un prix normé
(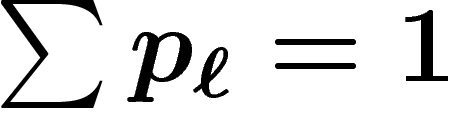 ) et où
) et où 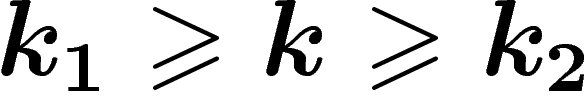 .
.
On considére sur E la fonction suivante :
![\[f :
(p,k) \mapsto \left(
\begin{array}{l}
\left(\displaystyle
\frac{p_\ell + \max\left(0, z_\ell\left(p,k\right)\right)}{1+\sum_m
\max\left(0, z_m\left(p,k\right)\right)}
\right)_\ell\, ,
\\
\max\left(k_2, \min \left(k_1, k\left(1+p.z\left(p,k\right)\right)\right)\right)
\end{array}
\right)
\]](prix057.png)
Par construction, cette fonction va bien de E dans E.
E est homéomorphe à une boule 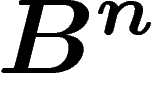 où n est le nombre de
biens. De plus, f est continue. Par conséquent, on
peut appliquer le théorème de Brouwer qui affirme que f a un point
fixe.
où n est le nombre de
biens. De plus, f est continue. Par conséquent, on
peut appliquer le théorème de Brouwer qui affirme que f a un point
fixe.
Soit 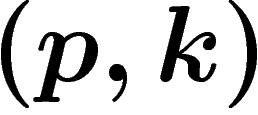 un point fixe de f. Montrons que
un point fixe de f. Montrons que
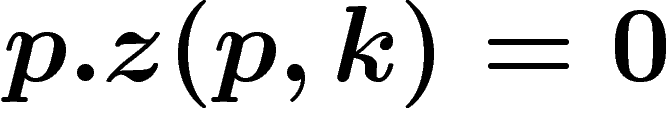 . D'abord, si k n'est ni
. D'abord, si k n'est ni 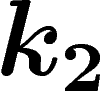 ni
ni 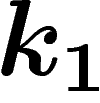 , le fait que
, le fait que
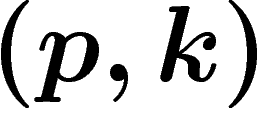 soit un point fixe implique que
soit un point fixe implique que 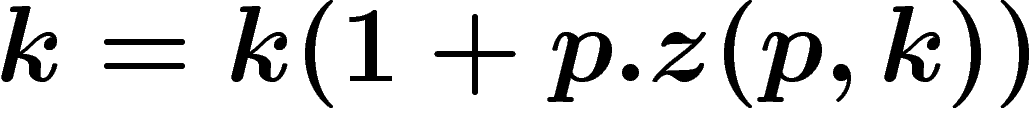 , donc
, donc 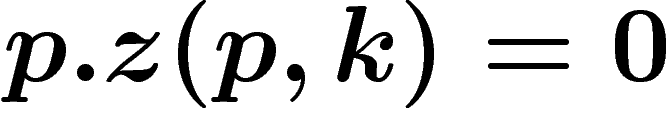 .
Sinon, si
.
Sinon, si 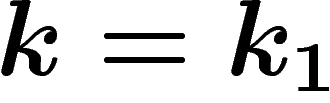 , comme on a
, comme on a 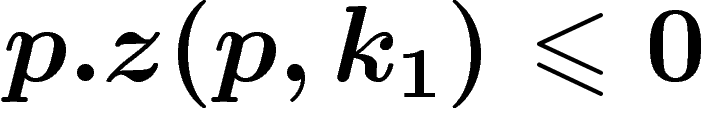 , et que
, et que 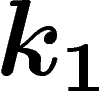 est fixe, cela signifie que
est fixe, cela signifie que 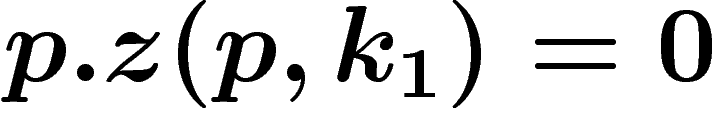 . De même si
. De même si
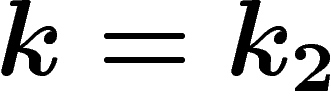 . Dans tous les cas,
. Dans tous les cas, 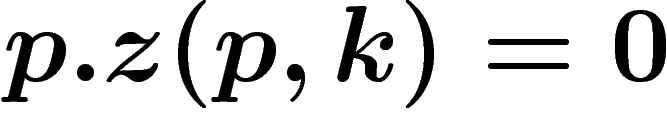 .
.
Maintenant, supposons qu'il existe un 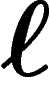 tel que
tel que
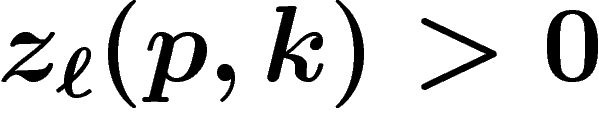 . Notons
. Notons 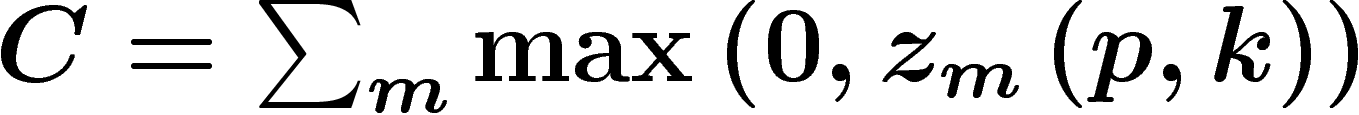 Comme on a supposé
Comme on a supposé
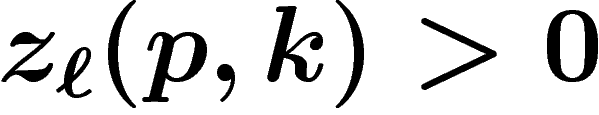 , on a
, on a 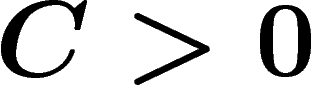 . Le fait que
. Le fait que 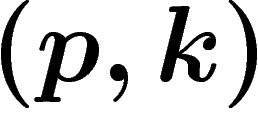 soit un
point fixe donne pour tout m
soit un
point fixe donne pour tout m
![\[
p_\ell=\frac{p_m + \max(0,z_m(p,k))}{1+C}
\]](prix078.png)
, soit encore ![\[\max(0,z_m(p,k))=C\, p_m\]](prix079.png)
.
Comme 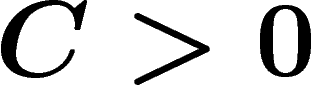 , on a donc
, on a donc 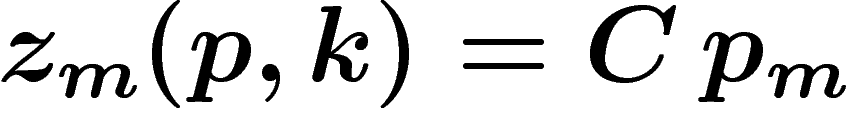 . Alors
. Alors
![\[
p.z(p,k)=\sum_m p_m \, z_m (p,k) = \sum_m C\, p_m^2
\]](prix082.png)
Or on a démontré que 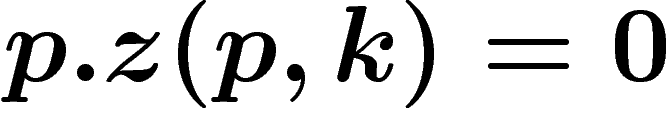 . Ceci implique
. Ceci implique 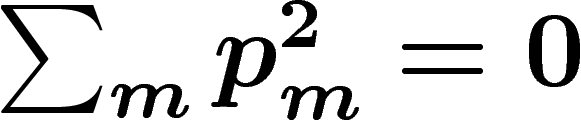 , ce
qui est absurde (l'hypothèse de demande strictement croissante
strictement convexe implique que les prix ne sont pas nuls).
, ce
qui est absurde (l'hypothèse de demande strictement croissante
strictement convexe implique que les prix ne sont pas nuls).
Donc l'hypothèse qu'il existe un 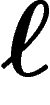 tel que
tel que 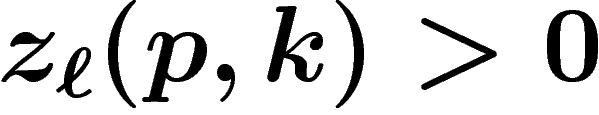 est
fausse. Tous les
est
fausse. Tous les 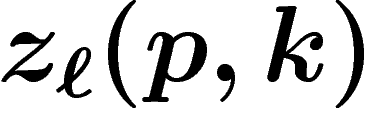 sont donc
sont donc 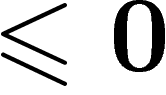 . Comme
. Comme 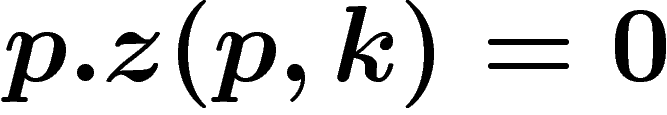 ,
ils ne peuvent être strictement négatifs, et donc
,
ils ne peuvent être strictement négatifs, et donc
![\[
\forall \ell, z_\ell(p,k)=0
\]](prix090.png)
ce qui signifie que le marché est en équilibre, et que toutes les
ressources sont attribuées.
Back to: Main Page > Économie, Politique
To leave a comment: contact (domain) yann-ollivier.org
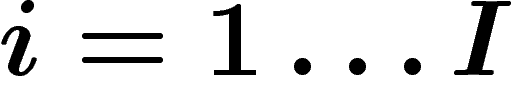 , et des biens
, et des biens 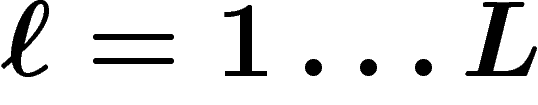 . Chaque individu i
possède un budget
. Chaque individu i
possède un budget  . Le bien
. Le bien 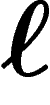 est présent sur le marché en
quantité
est présent sur le marché en
quantité 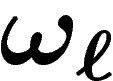 . On suppose que le
prix du bien
. On suppose que le
prix du bien 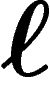 sur le marché est
sur le marché est 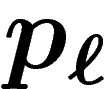 . On convient que l'individu
i, voulant acquérir une unité du bien
. On convient que l'individu
i, voulant acquérir une unité du bien 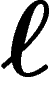 , paie non pas
, paie non pas 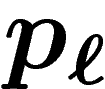 mais
mais 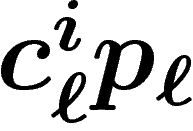 ,
, 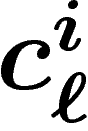 étant un nombre dépendant de
l'acheteur et du type de bien acheté (mais pas du vendeur).
étant un nombre dépendant de
l'acheteur et du type de bien acheté (mais pas du vendeur).
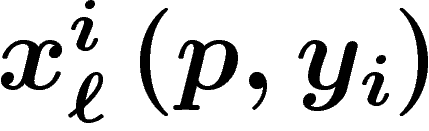 en les biens
en les biens 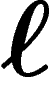 . La demande globale
en bien
. La demande globale
en bien 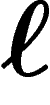 est
est 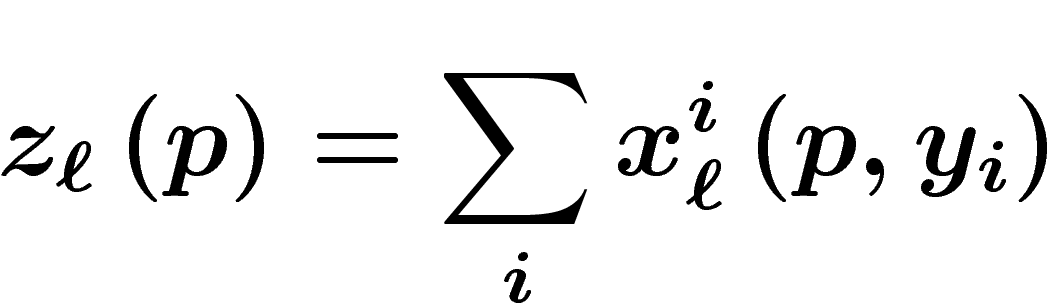 . Le marché est en équilibre si la demande
est égale à l'offre :
. Le marché est en équilibre si la demande
est égale à l'offre : 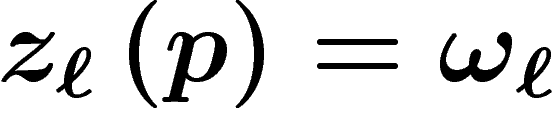 .
.
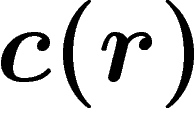 qu'il consacre à la consommation et à l'accroissement de son
bien-être, et la part
qu'il consacre à la consommation et à l'accroissement de son
bien-être, et la part 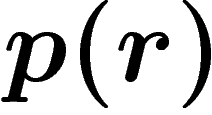 consacrée au positionnement. On prend la
valeur moyenne de ces quantités pour les ménages dont le revenu est
r. On ne veut pas toucher aux budgets de consommation, mais égaliser
les budgets de positionnement. Alors, on obtient immédiatement que le
coefficient de paiement d'un ménage ayant un revenu r doit être
consacrée au positionnement. On prend la
valeur moyenne de ces quantités pour les ménages dont le revenu est
r. On ne veut pas toucher aux budgets de consommation, mais égaliser
les budgets de positionnement. Alors, on obtient immédiatement que le
coefficient de paiement d'un ménage ayant un revenu r doit être  pour les produits de consommation (on ne change rien) et
pour les produits de consommation (on ne change rien) et 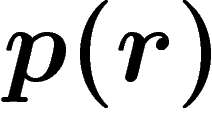 pour
les produits de positionnement (il paie plus s'il gagne plus, pas
proportionnellement à son revenu mais proportionnellement à la part de
son revenu qu'il consacrait auparavant à son positionnement).
pour
les produits de positionnement (il paie plus s'il gagne plus, pas
proportionnellement à son revenu mais proportionnellement à la part de
son revenu qu'il consacrait auparavant à son positionnement).
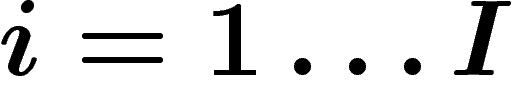 , et des biens
, et des biens 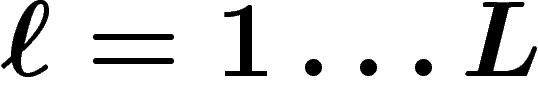 . Le bien
. Le bien 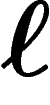 est
présent sur le marché en quantité
est
présent sur le marché en quantité 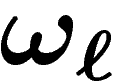 .
.
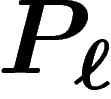 le prix du bien
le prix du bien 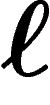 sur le marché. On décide qu'un
individu i, voulant acquérir une unité du bien
sur le marché. On décide qu'un
individu i, voulant acquérir une unité du bien 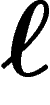 , paie non pas
, paie non pas
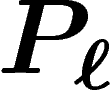 mais
mais 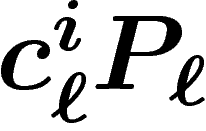 .
.
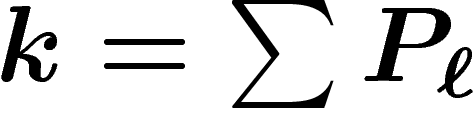 et
et
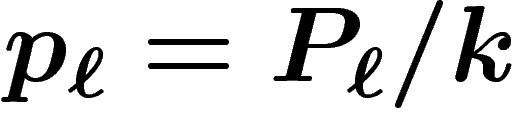 . On a ainsi
. On a ainsi 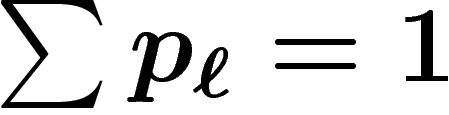 , et les prix sont
caractérisés par le couple
, et les prix sont
caractérisés par le couple 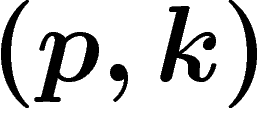 où p est normalisé.
où p est normalisé.
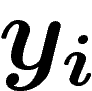 le budget de l'individu i. Soit
le budget de l'individu i. Soit
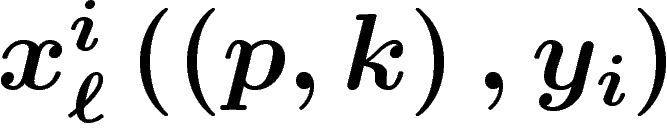 sa fonction de demande en
le bien
sa fonction de demande en
le bien 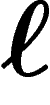 quand les prix sont
quand les prix sont 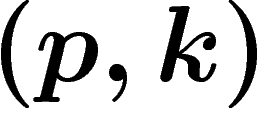 (c'est la même
que la fonction de demande habituelle quand on remplace
(c'est la même
que la fonction de demande habituelle quand on remplace
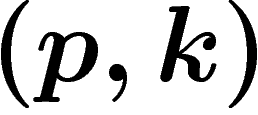 par le vecteur-prix
par le vecteur-prix 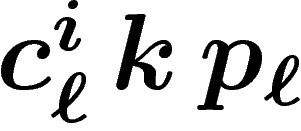 ).
).
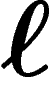 est
est 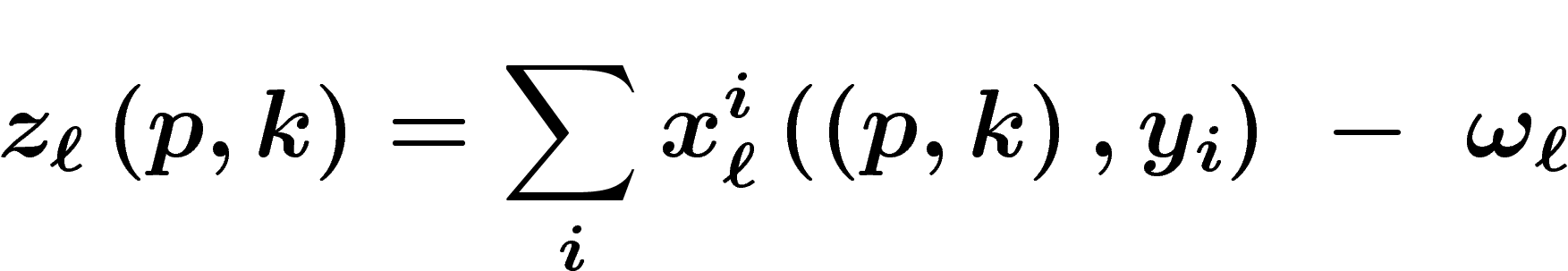 . Le marché du bien
. Le marché du bien 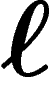 est en équilibre si et seulement si la demande est égale à l'offre :
est en équilibre si et seulement si la demande est égale à l'offre :
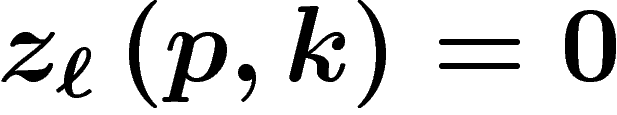 .
.
![\[\sum_\ell k\, p_\ell c_\ell^i \,
x_\ell^i\left(\left(p,k\right),y_i\right)=y_i
\]](prix044.png)
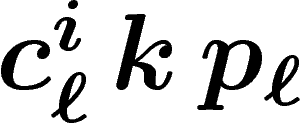 .)
.)
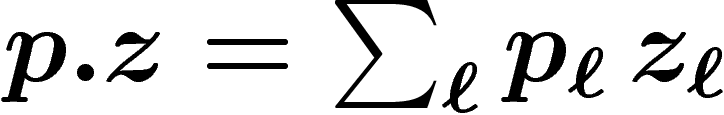 .
.
![\[k_1=\frac{1}{\min_{i,\ell}c^i_\ell} \frac{\sum_i y_i}
{\min_\ell \omega_\ell}
\ \mbox{ et } \ k_2=\frac{1}{\max_{i,\ell}c^i_\ell} \frac{\sum_i
y_i}{\max_\ell
\omega_\ell}\]](prix047.png)
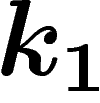 et
et 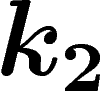 sont construits de telle sorte que si
sont construits de telle sorte que si  , on a
automatiquement
, on a
automatiquement  (les prix sont trop élevés) et que si
(les prix sont trop élevés) et que si 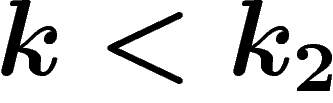 ,
on a
,
on a 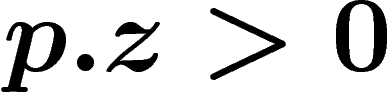 (les prix sont trop bas).
(les prix sont trop bas).
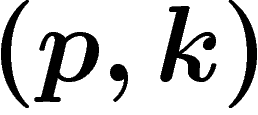 où p est un prix normé
(
où p est un prix normé
(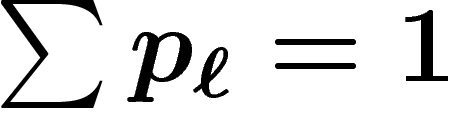 ) et où
) et où 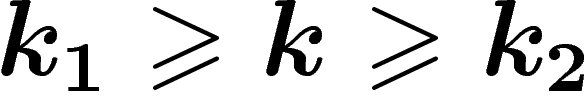 .
.
![\[f :
(p,k) \mapsto \left(
\begin{array}{l}
\left(\displaystyle
\frac{p_\ell + \max\left(0, z_\ell\left(p,k\right)\right)}{1+\sum_m
\max\left(0, z_m\left(p,k\right)\right)}
\right)_\ell\, ,
\\
\max\left(k_2, \min \left(k_1, k\left(1+p.z\left(p,k\right)\right)\right)\right)
\end{array}
\right)
\]](prix057.png)
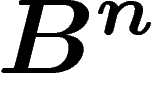 où n est le nombre de
biens. De plus, f est continue. Par conséquent, on
peut appliquer le théorème de Brouwer qui affirme que f a un point
fixe.
où n est le nombre de
biens. De plus, f est continue. Par conséquent, on
peut appliquer le théorème de Brouwer qui affirme que f a un point
fixe.
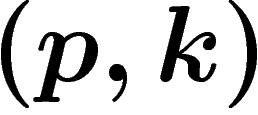 un point fixe de f. Montrons que
un point fixe de f. Montrons que
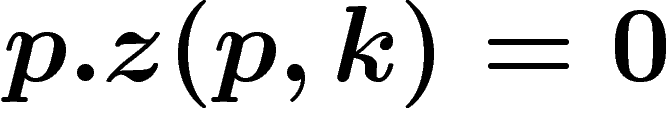 . D'abord, si k n'est ni
. D'abord, si k n'est ni 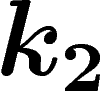 ni
ni 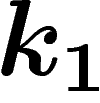 , le fait que
, le fait que
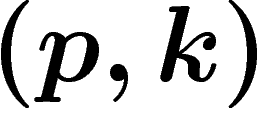 soit un point fixe implique que
soit un point fixe implique que 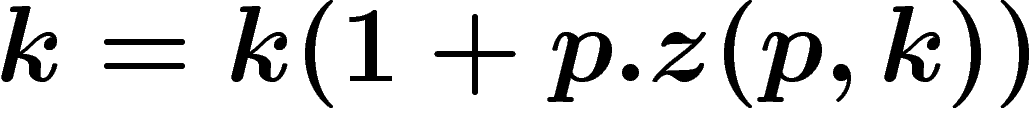 , donc
, donc 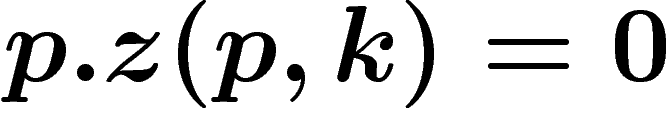 .
Sinon, si
.
Sinon, si 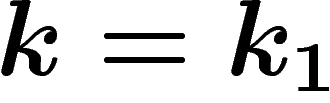 , comme on a
, comme on a 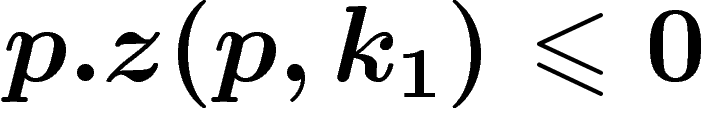 , et que
, et que 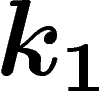 est fixe, cela signifie que
est fixe, cela signifie que 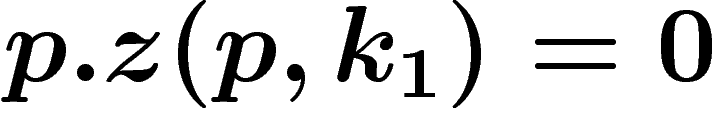 . De même si
. De même si
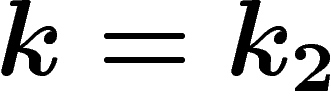 . Dans tous les cas,
. Dans tous les cas, 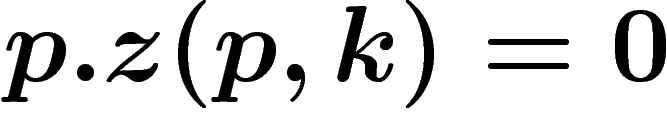 .
.
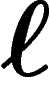 tel que
tel que
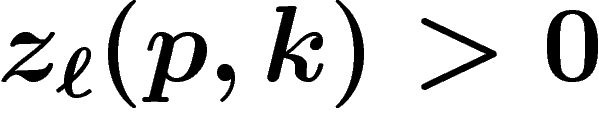 . Notons
. Notons 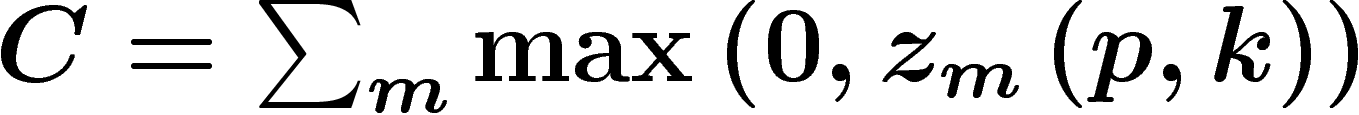 Comme on a supposé
Comme on a supposé
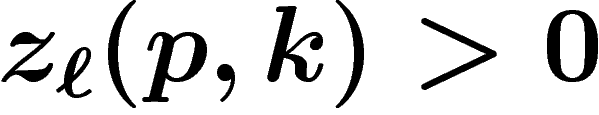 , on a
, on a 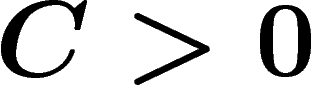 . Le fait que
. Le fait que 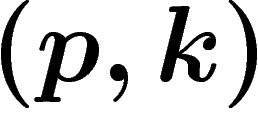 soit un
point fixe donne pour tout m
soit un
point fixe donne pour tout m ![\[
p_\ell=\frac{p_m + \max(0,z_m(p,k))}{1+C}
\]](prix078.png)
![\[\max(0,z_m(p,k))=C\, p_m\]](prix079.png)
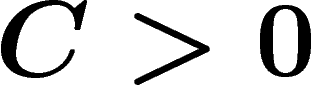 , on a donc
, on a donc 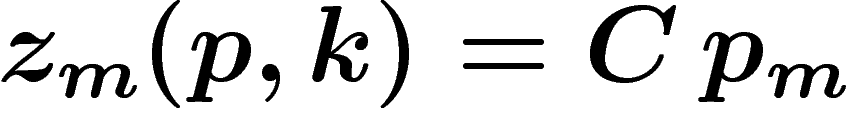 . Alors
. Alors ![\[
p.z(p,k)=\sum_m p_m \, z_m (p,k) = \sum_m C\, p_m^2
\]](prix082.png)
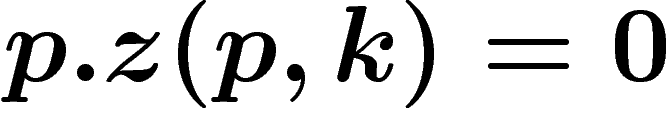 . Ceci implique
. Ceci implique 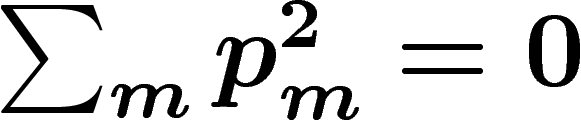 , ce
qui est absurde (l'hypothèse de demande strictement croissante
strictement convexe implique que les prix ne sont pas nuls).
, ce
qui est absurde (l'hypothèse de demande strictement croissante
strictement convexe implique que les prix ne sont pas nuls).
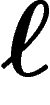 tel que
tel que 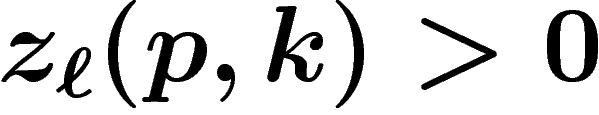 est
fausse. Tous les
est
fausse. Tous les 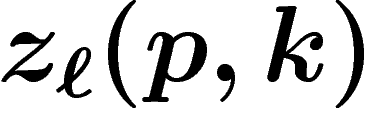 sont donc
sont donc 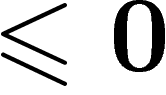 . Comme
. Comme 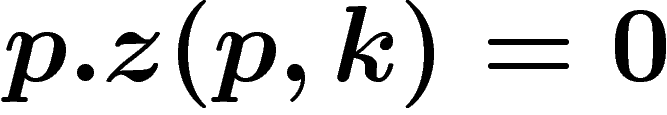 ,
ils ne peuvent être strictement négatifs, et donc
,
ils ne peuvent être strictement négatifs, et donc ![\[
\forall \ell, z_\ell(p,k)=0
\]](prix090.png)